للوصول السريع إلى الدروس والاختبارات..

حمل تطبيق دراستي من متجر جوجل

مبرهنة ذات الحدين

هي قانون لإيجاد ناتج قوی مجموع حدين أي مقدار مكون من مجموع حدين مثل (x+y) مرفوع إلى أس صحيح موجب.

ملاحظة:

لإيجاد مجموع حدين مرفوع إلى أي أس صحيح نستخدم القانون الآتي:

$(x + y)^{n} = C_{0}^{n} x^{n} + C_{1}^{n} x^{n - 1} y + c_{2}^{n} x^{n - 2} y^{2} + \dots + C_{n}^{n} y^{n}$

ملاحظات:

أس المتغير x يبدأ بالتناقص من n إلى 0 وأس المتغير y يبدأ بالتزايد من 0 إلى n.
إذا كانت الإشارة بين الحدين موجبة تتكون جميع إشارات الحدود موجبة.
إذا كانت الإشارة بين الحدين سالبة فهنا الإشارة تتناوب ما بين السالب والموجب أي أن الحد الأول سالب ثم الحد الثاني موجب وهكذا.
عدد حدود المفكوك = 1+n.

ملاحظة:

إذا كانت صيغة السؤال بسط المقدار

$(x + y)^{n} + (x - y)^{n}$ فهنا عند الحل نأخذ ضعف الحدود الفردية وتحذف الحدود الزوجية أي إذا كانت الإشارة بين القوسين موجية.
أما إذا كانت الإشارة بين القوسين سالبة $(x + y)^{n} - (x - y)^{n}$ فهنا عند الحل نأخذ ضعف الحدود الزوجية وتحذف الحدود الفردية.

1- جد مفكوك $(x - y)^{5}$ ؟

$\begin{aligned} (x - y)^{5} & = C_{0}^{5} x^{5} - C_{1}^{5} x^{4} \cdot y + C_{2}^{5} x^{3} \cdot y^{2} - C_{3}^{5} x^{2} \cdot y^{3} + C_{4}^{5} x \cdot y^{4} - C_{5}^{5} y^{5} \\ = x^{5} - 5 x^{4} y + \frac{5 \times 4}{2 \times 1} x^{3} \cdot y^{2} - \frac{5 \times 4 \times 3}{3 \times 2 \times 1} x^{2} y^{3} + 5 x y^{4} - y^{5} \\ = x^{5} - 5 x^{4} y + 10 x^{3} y^{2} - 10 x^{2} y^{3} + 5 x y^{4} - y^{5} \end{aligned}$

2- جد مفكوك $(3 a + b)^{4}$ ؟

$\begin{aligned} (3 a + b)^{4} & = c_{0}^{4} (3 a)^{4} + C_{1}^{4} (3 a)^{3} \cdot b + C_{2}^{4} (3 a)^{2} b^{2} + C_{3}^{4} (3 a) b^{3} + c_{4}^{4} b^{4} \\ = 81 a^{4} + 4 (27 a^{3}) \cdot b + \frac{4 \times 3}{2 \times 1} (9 a^{2}) b^{2} + 4 (3 a) b^{3} + b^{4} \\ = 81 a^{4} + 108 a^{3} \cdot b + 54 a^{2} \cdot b^{2} + 12 a \cdot b^{3} + b^{4} \end{aligned}$

3- جد قيمة $(101)^{3}$ ؟

نضع العدد 101 بصورة حدين 1+100

$\begin{aligned} (100 + 1)^{3} & = C_{0}^{3} (100)^{3} + C_{1}^{3} (100)^{2} (1) + C_{2}^{3} (100) (1)^{2} + C_{3}^{3} (1)^{3} \\ = 1000000 + 3 (10000) + 3 (100) + 1 \\ = 1000000 + 300000 + 300 + 1 \\ = 1030301 \end{aligned}$

4- بسط المقدار $(2 + \sqrt{3})^{4} + (2 - \sqrt{3})^{4}$ ؟

$\begin{aligned} (2 + \sqrt{3})^{4} & = C_{0}^{4} (2)^{4} + C_{1}^{4} (2)^{3} (\sqrt{3}) + C_{2}^{4} (2)^{2} \cdot (\sqrt{3})^{2} + C_{3}^{4} (2) (\sqrt{3})^{3} + C_{4}^{4} (\sqrt{3})^{4} \\ = 2 [P 1 + P 3 + P 5] \\ = 2 [C_{0}^{4} (2)^{4} + C_{2}^{4} (2)^{2} \cdot (\sqrt{3})^{2} + C_{4}^{4} (\sqrt{3})^{4}] \\ = 2 [16 + \frac{4 \times 3}{2 \times 1} (4) (3) + 9] = 2 [16 + 72 + 9] = 2 [25 + 72] \\ = 2 (97) = 194 \end{aligned}$

5- بسط المقدار ${(a + \frac{1}{a})}^{5} - {(a - \frac{1}{a})}^{5}$ ؟

$\begin{aligned} {(a + \frac{1}{a})}^{5} & = C_{0}^{5} a^{5} + C_{1}^{5} a^{4} \cdot \frac{1}{a} + C_{2}^{5} a^{3} \cdot {(\frac{1}{a})}^{2} + C_{3}^{5} a^{2} \cdot {(\frac{1}{a})}^{3} + C_{4}^{5} a \cdot {(\frac{1}{a})}^{4} C_{5}^{5} {(\frac{1}{a})}^{5} \\ = 2 [P 2 + P 4 + P 6] \\ = 2 [C_{1}^{5} a^{4} \cdot \frac{1}{a} + C_{3}^{5} a^{2} \cdot {(\frac{1}{a})}^{3} + C_{5}^{5} {(\frac{1}{a})}^{5}] \\ = 2 [5 a^{3} + \frac{5 \times 4 \times 3}{3 \times 2 \times 1} a^{2} \cdot \frac{1}{a^{3}} + \frac{1}{a^{5}}] \\ = 2 [5 a^{3} + \frac{10}{a} + \frac{1}{a^{5}}] \end{aligned}$

ملاحظات:

معامل كل حد رتبة r في مفكوك $(x + y)^{n}$ هو $C_{n - r}^{n}$ مثلاً معامل الحد السابع في مفكوك $(x + y)^{8}$ هو $C_{7 - 1}^{8}$

لإيجاد رتبة الحد الأوسط نطبق القانون الآتي $\frac{n}{2} + 1$

لإيجاد رتبة الحدين الأوسطين نطبق القوانين الآتية: $r 1 = \frac{n + 1}{2}, r 2 = \frac{n + 1}{2} + 1$

لإيجاد أي حد في مفكوك $(x + y)^{n}$ نطبق قانون الحد العام $\Pr = C_{r - 1}^{n} x^{n - r + 1} y^{r - 1}$

أي نستخدم قانون الحد العام في الحالات التالية:

لإيجاد قيمة الحد إذا علمت رتبته.
لإيجاد رتبة الحد إذا علمت قيمته.
إيجاد الحد الخالي من x أو الحد الحاوي.

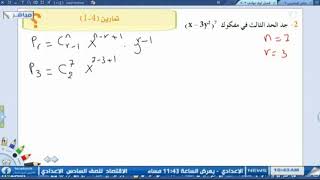
6- أوجد الحد الخامس في مفكوك $(x - 3 y)^{8}$ ؟

$\begin{aligned} P r & = C_{r - 1}^{n} x^{n - r + 1} y^{r - 1} \\ P 5 & = C_{5 - 1}^{8} x^{8 - 5 + 1} \cdot (- 3 y)^{5 - 1} \\ P 5 & = \frac{8 \times 7 \times 6 \times 4}{4 \times 3 \times 2 \times 1} x^{4} \cdot (- 3 y)^{4} = 70 x^{4} (81 y^{4}) \\ = 5670 x^{4} \cdot y^{4} \end{aligned}$

7- أوجد الحد الأوسط في مفكوك ${(\frac{x}{2} - 3)}^{8}$ .

$\begin{aligned} r & = \frac{n}{2} + 1 = \frac{8}{2} + 1 = 5 \\ P r & = C_{r - 1}^{n} x^{n - r + 1} y^{r - 1} \\ P 5 & = C_{5 - 1}^{8} {(\frac{x}{2})}^{8 - 5 + 1} (- 3)^{5 - 1} \\ = \frac{8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1} {(\frac{x}{2})}^{4} \cdot (- 3)^{4} \\ = 70 \times \frac{x^{4}}{16} \times 81 = \frac{2835}{8} x^{4} \end{aligned}$

8- جد الحدين الأوسطين في مفكوك ${(\frac{3 a}{2} - \frac{2}{3 a})}^{7}$

$r 1 = \frac{n + 1}{2} = \frac{7 + 1}{2} = 4, r 2 = \frac{n + 1}{2} + 1 = \frac{7 + 1}{2} + 1 = 5 \begin{aligned} P r = C_{r - 1}^{n} x^{n - r + 1} y^{r - 1} \\ P_{4} = C_{4 - 1}^{7} {(\frac{3 a}{2})}^{7 - 4 + 1} \cdot {(\frac{- 2}{3 a})}^{4 - 1} ⟹ \frac{7 \times 6 \times 5}{3 \times 2 \times 1} {(\frac{3 a}{2})}^{4} \cdot {(\frac{- 2}{3 a})}^{3} \\ P 4 = 35 \cdot \frac{81 a^{4}}{16} \cdot \frac{- 8}{27 a^{3}} ⟹= \frac{- 105 a}{2} \\ P_{5} = C_{5 - 1}^{7} \cdot {(\frac{3 a}{2})}^{7 - 5 + 1} \cdot {(\frac{- 2}{3 a})}^{5 - 1} ⟹= \frac{7 \times 6 \times 5 \times 4}{4 \times 3 \times 2 \times 1} \cdot {(\frac{3 a}{2})}^{3} \cdot {(\frac{- 2}{3 a})}^{4} \\ = 35 \cdot \frac{27 a^{3}}{8} \cdot \frac{16}{81 a^{4}} = \frac{70}{3 a} \end{aligned}$

9- جد الحد الذي يحوي على $a^{8}$ في مفكوك ${(3 + a^{2})}^{8}$ ثم جد معامله؟

$\begin{aligned} P r = C_{r - 1}^{n} x^{n - r + 1} y^{r - 1} \\ P r = C_{r - 1}^{8} (3)^{8 - r + 1} \cdot {(a^{2})}^{r - 1} ⟹ a^{2 r - 2} = a^{8} ⟹ 2 r - 2 = 8 \\ 2 r = 10] \div 2 ⟹ r = 5 \\ P 5 = C_{5 - 1}^{8} (3)^{8 - 5 + 1} {(a^{2})}^{5 - 1} ⟹ \frac{8 \times 7 \times 6 \times 5}{4 \times 2 \times 2 \times 1} (3)^{4} {(a^{2})}^{4} = 70 (81) a^{8} = 5670 a^{8} \\ 5670 معاملة \end{aligned}$

10- جد الحد الخالي من (x) في مفكوك ${(x^{2} - \frac{1}{x})}^{15}$ ؟

نفرض أن رتبة الحد الخالي من x أي يحتوي على x⁰ هو r

$\begin{aligned} \Pr = C_{r - 1}^{15} {(x^{2})}^{15 - r + 1} {(- \frac{1}{x})}^{r - 1} ⟹= C_{r - 1}^{15} {(x^{2})}^{16 - r} (- 1)^{r - 1} {(x^{- 1})}^{r - 1} \\ C_{r - 1}^{15} x^{32 - 2 r} (- 1)^{r - 1} x^{- r + 1} \\ x^{32 - 2 r} . x^{- r + 1} = x^{0} ⟹ x^{33 - 3 r} = x^{0} ⟹ 33 - 3 r = 0] \div 3 \Rightarrow r = 11 \\ P 11 = C_{11 - 1}^{15} x^{32 - 22} (- 1)^{11 - 1} x^{- 11 + 1} = C_{10}^{15} x^{10} \cdot x^{- 10} \\ = \frac{15!}{10! \times 5!} = \frac{15 \times 14 \times 13 \times 12 \times 11 \times 10!}{10! \times 5!} \\ = \frac{15 \times 14 \times 13 \times 12 \times 11^{10} = 3 \times 7 \times 13 \times 11 = 3003}{5 \times 4 \times 3 \times 2 \times 1} = 3 \end{aligned}$

للوصول السريع إلى الدروس والاختبارات..

حمل تطبيق دراستي من متجر جوجل

فايسبوك

واتساب

تيليجرام

طباعة

شرح فيديو

للوصول السريع إلى الدروس والاختبارات..

مبرهنة ذات الحدين

1- جد مفكوك $(x - y)^{5}$ ؟

2- جد مفكوك $(3 a + b)^{4}$ ؟

3- جد قيمة $(101)^{3}$ ؟

4- بسط المقدار $(2 + \sqrt{3})^{4} + (2 - \sqrt{3})^{4}$ ؟

5- بسط المقدار ${(a + \frac{1}{a})}^{5} - {(a - \frac{1}{a})}^{5}$ ؟

6- أوجد الحد الخامس في مفكوك $(x - 3 y)^{8}$ ؟

7- أوجد الحد الأوسط في مفكوك ${(\frac{x}{2} - 3)}^{8}$ .

8- جد الحدين الأوسطين في مفكوك ${(\frac{3 a}{2} - \frac{2}{3 a})}^{7}$

9- جد الحد الذي يحوي على $a^{8}$ في مفكوك ${(3 + a^{2})}^{8}$ ثم جد معامله؟

10- جد الحد الخالي من (x) في مفكوك ${(x^{2} - \frac{1}{x})}^{15}$ ؟

للوصول السريع إلى الدروس والاختبارات..

مشاركة

شرح فيديو

فيديو شرح درس مبرهنة ذات الحدين

النقاشات

للوصول السريع إلى الدروس والاختبارات..

مبرهنة ذات الحدين

1- جد مفكوك (x−y)5؟

2- جد مفكوك (3a+b)4؟

3- جد قيمة (101)3؟

4- بسط المقدار (2+3)4+(2−3)4؟

5- بسط المقدار (a+1a)5−(a−1a)5؟

6- أوجد الحد الخامس في مفكوك (x−3y)8؟

7- أوجد الحد الأوسط في مفكوك (x2−3)8.

8- جد الحدين الأوسطين في مفكوك (3a2−23a)7

9- جد الحد الذي يحوي على a8 في مفكوك (3+a2)8 ثم جد معامله؟

10- جد الحد الخالي من (x) في مفكوك (x2−1x)15؟

للوصول السريع إلى الدروس والاختبارات..

مشاركة

شرح فيديو

فيديو شرح درس مبرهنة ذات الحدين

النقاشات

1- جد مفكوك $(x - y)^{5}$ ؟

2- جد مفكوك $(3 a + b)^{4}$ ؟

3- جد قيمة $(101)^{3}$ ؟

4- بسط المقدار $(2 + \sqrt{3})^{4} + (2 - \sqrt{3})^{4}$ ؟

5- بسط المقدار ${(a + \frac{1}{a})}^{5} - {(a - \frac{1}{a})}^{5}$ ؟

6- أوجد الحد الخامس في مفكوك $(x - 3 y)^{8}$ ؟

7- أوجد الحد الأوسط في مفكوك ${(\frac{x}{2} - 3)}^{8}$ .

8- جد الحدين الأوسطين في مفكوك ${(\frac{3 a}{2} - \frac{2}{3 a})}^{7}$

9- جد الحد الذي يحوي على $a^{8}$ في مفكوك ${(3 + a^{2})}^{8}$ ثم جد معامله؟

10- جد الحد الخالي من (x) في مفكوك ${(x^{2} - \frac{1}{x})}^{15}$ ؟