حلول أسئلة الصف السادس الإعدادي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى
المعدلات المرتبطة بالزمن (المعدلات الزمنية)
المعدلات المرتبطة بالزمن (المعدلات الزمنية)
إذا وجد أكثر من متغير بحيث تتوقف كل من هذه المتغيرات على متغير واحد ومثاله الزمن فتتغير كل المتغيرات تبعاً لتغيره حيث هنا يكون الاشتقاق دائماً بالنسبة للزمن ، فمنها المتغيرات متغيرين تابعين كل منهما مرتبط بالمتغير المستقل .
ملاحظات لحل أي سؤال يتعلق بالمعادلات المرتبطة بالزمن نتبع ما يأتي:
- سوف تقسم العلاقات إلى نوعين (علاقات أساسية) وهي علاقات يتم اشتقاقها و(علاقات ثانوية) وهي علاقة يتم من خلالها تقليص عدد المتغيرات في السؤال.
- الثابت الدائم يعوض قبل الاشتقاق والمتغير الدائم يعوض بعد الاشتقاق وأحياناً نقوم بتعويضه قبل الاشتقاق وذلك لإيجاد قيمة متغير دائم آخر.
- كلمة معدل أو سرعة أو بعد من الأبعاد معناه الآتي: ويكون موجباً في حالة التزايد وسالباً في حالة التناقص.
- عند الاشتقاق بالنسبة إلى الزمن يكون كالآتي: معدل تغير الحجم أو معدل تغير نصف القطر إلخ.
- إذا طلب في السؤال معدل تغير قانون لشكل هندسي فإن ذلك القانون يكون علاقة أساسية.
(1)- مكعب من الثلج يذوب بالحرارة بحيث يحافظ على شكله مكعباً فإذا كان معدل تغير حجمه يساوي جد معدل تغير مساحته السطحية في اللحظة التي يكون طول حرفه
نفرض:
- طول الضلع =
- نفرض حجم المكعب =
- نفرض المساحة السطحية =
- معدل التغير بالمساحة =
- معدل التغير بالحجم =
- معدل التغير الطول =
جد م المكعب =
المساحة السطحية للمكعب = 6 × ,
معدل تغير المساحة السطحية:
أو تكتب كالآتي:
معدل نقصان المساحة السطحية
(2)- مرشح مخروطي قاعدته أفقية ورأسه للأسفل ارتفاعه يساوي وطول قطر قاعدته يصب فيه سائل بمعدل بينما يترسب من السائل بمعدل جد معدل تغير عمق السائل في اللحظة التي يكون فيها عمق السائل
نفرض:
- نصف قطر القاعدة =
- حجم السائل =
- ارتفاع السائل =
- معدل تغير ارتفاع السائل =
- معد تغير حجم السائل =
نعوض معادلة (1) في معادلة (2):
معدل تغير حجم السائل في المخروط = معدل الصب - معدل التسرب
نعوض معدل تغير الحجم في معادلة (3)
(3)- لتكن نقطة متحركة على منحني القطع المكافئ بحيث يكون معدل ابتعادها عن النقطة يساوي جد معدل التغير الزمني للإحداثي السيني للنقطة عندما يكون
نفرض:
لتكن النقطة للقطع المكافئ
لتكن النقطة
المسافة بين
معدل الابتعاد =
معدل تغير الإحداثي السيني =
(4)- خزان مملوء بالماء على شكل متوازي سطوح مستطيلة قاعدته مربعة طولها يتسرب منه الماء بمعدل جد معدل انخفاض الماء في الخزان عند أي زمن
نفرض:
- حجم الماء في الخزان =
- ارتفاع الماء في الخزان =
- مساحة القاعدة المربعة =
- طول ضلع القاعدة المربعة =
- معدل انخفاض الماء في الخزان =
- معدل تسرب الماء من الخزان =
إن الماء يأخذ شكل متوازي سطوح مستطيلة قاعدته مربعة.
معدل تغير انخفاض الماء في الخزان =
(5)- صفيحة مستطيلة من المعدن مساحتها يتمدد طولها بمعدل بحيث تبقى مساحتها ثابتة جد معدل النقصان في عرضها وذلك عندما يكون عرضها
نفرض:
- طول المستطيل =
- عرض المستطيل =
- معدل التغير بالطول =
- معدل تغير العرض =
نشتق طرفي معادلة (1) بالنسبة إلى الزمن
معدل التناقص في عرض المستطيل =
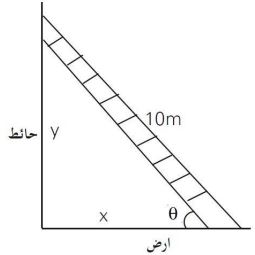
(6)- سلم طوله يستند طرفه الأسفل على أرض أفقية وطرفه العلوي على حائط رأسي فإذا انزلق الطرف الأسفل مبتعداً عن الحائط بمعدل عندما يكون الطرف الأسفل على بعد عن الحائط جد:
معدل انزلاق الطرف العلوي
نفرض:
- بعد الطرف الأسفل عن الحائط =
- بعد الطرف الأعلى عن الأرض =
- قياس الزاوية بين السلم والأرض =
- معدل تغير بعد الطرف الأسفل عن الحائط =
- معدل تغير بعد الطرف العلوي عن الأرض =
- سرعة تغير الزاوية =
معدل انزلاق الطرف العلوي =
سرعة تغير الزاوية بين السلم والأرض:
نعوض
نعوض
فتكون سرعة تغير الزاوية بين السلم والأرض
(7)- نقطة تتحرك على الدائرة فإذا كان معدل تغير الإحداثي السيني لها عند النقطة جد معدل التغير في الإحداثي الصادي عند نفس النقطة.
نفرض:
- معدل تغير الإحداثي السيني =
- معدل تغير الإحداثي الصادي =
النقطة
(8)- مكعب طول حرفه مغطى بطبقة من الجليد بحيث شكله يبقى مكعب، فإذا بدأ الجليد بالذوبان بمعدل فجد معدل النقصان بسمك الجليد في اللحظة التي يكون فيها هذا السمك =
نفرض:
- سمك الجليد =
- حجم الجليد =
- معدل نقصان سمك الجليد =
- سمك الجليد =
- معدل تغير حجم الجليد =
حجم الجليد = حجم المكعب المغطى بالجليد - حجم المكعب الأصلي
معدل النقصان في سمك الجليد =
حلول أسئلة الصف السادس الإعدادي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى


.JPG)
.JPG)
.JPG)




النقاشات