للوصول السريع إلى الدروس والاختبارات..
حمل تطبيق دراستي من متجر جوجل

تمارين (2-6)
(1)- برهن أن طول قطعة المستقيم الموازي لمستوٍ معلوم يساوي طول مسقطه على المستوي المعلوم ويوازيه.
المعطيات: ، مسقط على
المطلوب إثباته:
البرهان:
- مسقط على (معطی).
- (حسب تعريف مسقط قطعة مستقيم).
- (المستقيمان العموديان على مستو واحد متوازيان).
- لیكن مستوي المستقيمين المتوازيين (لكل مستقيمين متوازيين يوجد مستو وحيد يحتويهما).
- (معطی).
- (مستقيم تقاطع مستويين يوازي كل مستقيم محتوى في أحدهما ويوازي الآخر) (و. هـ. م) (1).
- الشكل متوازي أضلاع (يكون الشكل الرباعي متوازي إذا كان فيه كل ضلعين متقابلين فيه متوازيين).
- (متوازي الأضلاع يكون فيه كل ضلعين متقابلين متطابقين) (و. هـ. م) (2).
(2)- برهن أنه إذا قطع مستويان متوازيان بمستقيم فإنه ميله على أحدهما يساوي ميله على الآخر.
المعطيات:
- يقطع في النقطتين على الترتيب.
المطلوب إثباته: زاوية ميل على = زاوية ميل على .
البرهان: نرسم (في المستوى الواحد يمكن رسم مستقيم وحيد عمودي على مستوٍ معلوم من نقطة معلومة).
- (معطی).
- (المستقيم العمودي على أحد مستويين متوازيين يكون عمودياً على الآخر).
- يعينان المستوي (لكل مستقيمين متقاطعين يوجد مستو وحيد يحتويهما).
- (يتقاطع المستويين بمستقيم).
- (خطأ تقاطع مستويين متوازيين بمستو ثالث متوازيان).
- هي زاوية ميل على ، هي زاوية ميل على
- (زاوية الميل هي الزاوية المحددة بالمائل ومسقطه على المستوي).
- (بالتناظر).
- زاوية ميل على = ميل على (و. هـ. م).
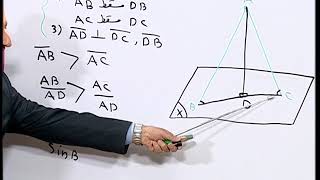
(3)- يرهن على أن للمستقيمات المتوازية المائلة على مستوي الميل نفسه.
المعطيات: وكل منهما مائلان على
المطلوب إثباته: زاوية ميل على = زاوية ميل على
البرهان: نرسم
- (يمكن رسم مستقيم وحيد عمودي على مستو من نقطة معلومة).
- مسقط على
- مسقط على
(تعريف مسقط قطعة مستقيم على المستوي).
- قائما الزاوية في على الترتيب.
- (المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المرسومة من أثره).
- (المستقيمان العموديان على مستو واحد متوازيان).
- (معطى).
- (إذا وازی ضلعا زاوية ضلعي زاوية أخرى تساوى قياسهما وتوازي مستويهما).
- (لأنه مثلث قائم الزاوية).
- (مجموع قياسات زوايا المثلث = ) (و. هـ. م).
(4)- برهن على أنه إذا رسم مائلان مختلفان في الطول من نقطة لا تنتمي إلى مستوي معلوم فإن أطولهما زاوية ميله على المستوي أصغر من زاوية ميل الآخر عليه.
المعطيات:
- مائلان على
المطلوب إثباته: قياس زاوية < قياس زاوية
البرهان: نرسم (يمكن رسم مستقيم وحيد عمودي على مستوي معلوم من نقطة معلومة).
- نصل
- مسقط على
- مسقط على
- (مسقط قطعة مستقيم غير عمودية على مستوٍ هو قطعة المستقيم الواصلة بين أثري العمودين النازلين على المستوي من طرف القطعة المستقيمة).
- هي زاوية ميل على
- هي زاوية ميل على
- (زاوية الميل هي الزاوية المحددة بالمائل ومسقطه على المستوي).
- (المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المرسومة من أثره).
- قائما الزاوية في .
- (معطى).
- (خواص التباين).
- قياس زاوية < قياس زاوية (و. هـ. م).
(5)- برهن على أنه إذا رسم مائلان من نقطة ما إلى مستوي فأصغرهما ميلاً هو الأطول.
المعطيات:
- مائلان على
- قياس زاوية < قياس زاوية
المطلوب إثباته:
البرهان: نرسم (يمكن رسم مستقيم وحيد عمودي على مستو معلوم من نقطة معلومة).
- نصل
- مسقط على
- مسقط على
- (مسقط قطعة مستقيم غير عمودية على مستو هو قطعة المستقيم الواصلة بين أثري العمودين النازلين على المستوي من طرف القطعة المستقيمة).
- هي زاوية ميل على
- هي زاوية ميل على
- (زاوية الميل هي الزاوية المحددة بالمائل ومسقطه على المستوي).
- (المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المرسومة من أثره).
- قائما الزاوية في .
- قياس زاوية < قياس زاوية (معطى).
- (خواص التباين) (و. هـ. م).
(6)- برهن أن زاوية الميل بين المستقيم ومسقطه على مستوٍ أصغر من الزاوية المحصورة بين المستقيم نفسه وأي مستقيم آخر مرسوم من موقعه ضمن ذلك المستوي.
المعطيات:
- مائل على ، مسقط على
- محددة بـ
- محددة بـ
المطلوب إثباته:
البرهان:
- لتكن بحيث أن ، نصل
- نرسم (يمكن رسم مستقيم وحيد عمودي على مستو معلوم من نقطة معلومة).
- (المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المرسومة من أثره).
- (العمود النازل من نقطة على مستوي هو أقصر مسافة بين النقطة المعلومة وأي نقطة أخرى تقع ضمن ذلك المستوي).
- مشترك، (بالبرهان).
- لتكن
- (إذا ساوى ضلعا مثلث ضلعي مثلث آخر واختلف الضلعان الآخران فأصغرهما يقابل أصغر الزاويتين) (و. هـ. م).
للوصول السريع إلى الدروس والاختبارات..
حمل تطبيق دراستي من متجر جوجل



.JPG)
.JPG)
.JPG)
.JPG)
.JPG)


النقاشات