حلول أسئلة الصف السادس الابتدائي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى
حل مسائل
.JPG)
١) تكفي كل علبة طلاءٍ منطقةً مساحتها ٦م٢، كم علبةً تلزم لطلاء حائطٍ طوله ٦م وعرضه ٣م؟
أفهم:
- المعطيات: تكفي علبة طلاءٍ واحدة منطقةً مساحتها ٦م.
- المطلوب: كم علبة طلاء تلزم لطلاء حائط طوله ٦م وعرضه ٣م.
أخطط: كيف يمكنني حل المسألة بالخطوات الاربع لإيجاد مساحة الحائط.
أحل: أستعمل قانون مساحة المستطيل.
- مساحة المستطيل = الطول × العرض.
- مساحة المستطيل = ٦ × ٣
- مساحة المستطيل = ١٨ م مربع.
١٨ ÷ ٦ = ٣ علب يلزم لطلاء الحائط.
أتحقق:
- بما أن مساحة الحائط ١٨ م مربع.
- نقسم مساحة الحائط على مساحة المنطقة الواحدة حتى نحصل على عدد العلب من الطلاء، لذا إجابتي معقولة.
٢) أرضية أحد صفوف المدرسة على شكل مستطيلٍ طوله ٤ م وعرضه ٣ م، يراد تبليطها باستعمال قطع بلاطٍ كل منها على شكل متوازي أضلاعٍ طول قاعدة كل منها ٣٠ سم وارتفاعها ٢٠ سم، كم قطعة بلاط يلزم لتبليط الصف؟
أفهم:
- المعطيات: طول وعرض أرضية الصف وطول قطع البلاط ٣٠ سم وارتفاعها ٢٠ سم.
- المطلوب: كم قطعة بلاط نحتاج لتبليط الصف.
أخطط:
كيف يمكنني استخدام خطوات حل المسألة الأربعة لإيجاد مساحة متوازي الأضلاع ومساحة المستطيل ويجب تساوي الوحدات.
أحل: ١ م = ١٠٠ سم.
- إذاً طول الصف = ٤ م × ١٠٠ = ٤٠٠ سم.
- عرض الصف = ٣ × ١٠٠ = ٣٠٠ سم.
- مساحة المستطيل = الطول × العرض.
- مساحة المستطيل = ٤٠٠ × ٣٠٠
- مساحة المستطيل = ١٢٠٠٠٠ سم مربع.
- الآن يجب إيجاد مساحة قطع البلاط.
- مساحة متوازي الأضلاع = الطول × العرض.
- = ٣٠ × ٢٠ = ٦٠٠ سم مربع مساحة قطعة البلاطة الواحدة.
عدد قطع البلاط = ١٢٠٠٠٠ ÷ ٦٠٠ = ٢٠٠ بلاطة تحتاج أرضية الصف.
أتحقق: مساحة المستطيل (أرضية الصف) أكبر من مساحة قطعة البلاطة الواحدة ب ٢٠٠ مرة، لذا إجابتي معقولة.
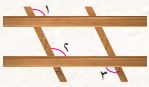
٣) الصورة المجاورة تبين جزءاً من سياج حقلٍ، أستعمل الزاوية ٢ لأجد علاقةً بين الزاويتين ١، ٣
أفهم:
- المعطيات: زاوية ١، وزاوية ٢، وزاوية ٣
- المطلوب: إيجاد العلاقة بين الزاويتين باستعمال الزاوية ١
أخطط: كيف يمكنني إيجاد العلاقة بين الزاويتين ١ و٣ بمعرفة العلاقة بين الزاويتين ١ و٢ والزاويتين ٢ و٣
أحل: بما أن الزاوية ١ والزاوية ٢ متناظرتان إذاً هما زاويتان متساويتان وبالتالي زاوية ١ = ٣
أتحقق: بما أن الزاويتين المتبادلتان والمتناظرتان متساويتان بالقياس فالزاويتان ١ و٣ متساويتان، لذا إجابتي معقولة.
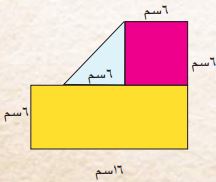
٤) أجد مساحة الشكل الهندسي المستوي المركب المجاور:
أفهم:
المعطيات: الشكل الهندسي المستوي مركب من عدة أشكال.
- أحد أبعاد الشكل المركب.
- طول وعرض المربع.
- طول وعرض المستطيل.
- طول وعرض المثلث.
المطلوب: مساحة الشكل الهندسي المركب.
أخطط: يمكنني إيجاد مساحة الشكل المستوي المركب بإيجاد مساحة كل شكل على حده (مساحة أجزاء الشكل المركب).
أحل:
- مساحة المربع = طول الضلع × نفسه.
- مساحة المربع = ٦ × ٦ = ٣٦ سم مربع.
- مساحة المثلث = × ٦ × ٦ = ١٨ سم مربع.
- الشكل المستطيل = الطول × العرض.
- الشكل المستطيل = ٦ × ١٦ = ٩٦ سم مربع.
- مساحة الشكل المستوي المركب = ٣٦ + ١٨ + ٩٦
- مساحة الشكل المستوي المركب = ١٥٠ سم مربع.
أتحقق: مساحة الشكل المستوي المركب أكبر من مساحة المربع والمثلث والمستطيل، لذا إجابتي معقولة.
حلول أسئلة الصف السادس الابتدائي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى
النقاشات