حلول أسئلة الصف الخامس الإعدادي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى
الدرس: 1-5 جمع المتجهات
جمع المتجهات: بما ان للكمية المتجهة مقدارًا و اتجاهًا , فعملية جمع المتجهات لا تخضع لقاعدة الجمع الجيري كما هو الحال في الكميات القياسية، وهنالك طريقتين لجمع المتجهات هما:
- الطريقة البيانية في جمع المتجهات ( طريقة ذيل برأس ):
من الممكن جمع متجهين بيانيًا وذلك برسم المتجه الأول ثم تضع ذيل المتجه عند رأس المتجه الأول فالمستقيم المرسوم من ذيل المتجه الاول الى رأس المتجه الثاني بمثل المتجه المحصل لهما. فمثلا لجمع المتجهين و بيانيا نقوم بتركيب ذيل احد المتجهين مثل المتجه على رأس متجه آخر مثل المتجه وبنفس مقياس الرسم مع المحافظة على اتجاهه ثم تصل بخط مستقيم بين ديل المتجه ورأس المتجه ويمثل الخط المستقيم متجه حاصل الجمع:
( المتجه المحصل ) ويسمى وهو مجموع المتجهين مقدارًا و اتجاهًا وهناك طريقة أخرى لعملية جمع المتجهين وفيما نرسم المتجه الثاني اولا ثم نضع ذيل المتجه عند رأس المتجه لاحظ ان المتجه المحصل في هذه الحالة هو المتجه نفسه مما يعني ان: اي أن جمع المتجهات يمتاز بخاصية الابدال وكذلك يمكن جمع المتجه مع نفسه بطريقة الرسم. فان متجه المحصلة في هذه الحالة هو:
وهنا هو المتجه المحصل مقداره يساوي ضعف مقدار المتجه وله اتجاه نفسه.
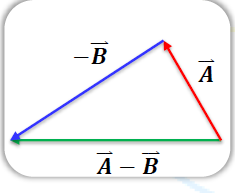
- طرح المتجهات: ان حاصل طرح متجهين هو نفسه حاصل جمع متجه وسالب متجه آخر:
فمثلا عملية طرح المتجهين و هي عملية جمع للمتجهين و أي ان:
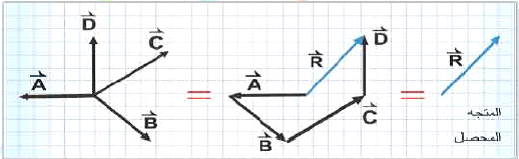
جمع ثلاث متجهات او اكثر: لجمع ثلاث متجهات او اكثر نبدأ من نقطة تأثير واحدة نضع ذيل المتجه الثاني عند رسم المتجه الاول وذيل المتجه الثاني عند رأس المتجه الثالث فالمستقيم الذي ذيله عند ذيل المتجه الاول ورأسه عند رأس المتجه المحصل للمتجهات .
 ملاحظات
ملاحظات
- جمع المتجهات يمتاز بخاصية الابدال اي ان:
- عند جمع اي متجه مع نفسه ينتج متجه محصل مقداره بساوي ضعف مقدار المتجه واتجاهه نفس اتجاه المتجهين. فمثلاً عند جمع المتجه مع نفسه فأن مقدار المتجه المحصل في هذه الحالة يساوي ضعف
- مقدار المتجه واتجاهه باتجاه .
- ان جمع المتجهات بطريقة الرسم تعتمد على نقل المتجه الى موقع اخر بحيث نحافظ على مقداره ويظل اتجاهه موازيًا للاتجاه الاصلي لذلك سوف نحصل على نفس المتجه.
تحليل المتجه
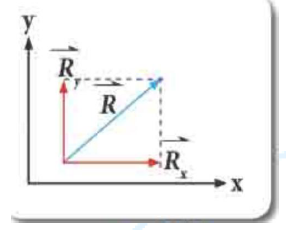
اي متجه يمكن ان يحلل الى متجهين ( مركبتين ) متعامدتين احداهما يوازي المحور ( X ) ويسمى المركبة الأفقية ويمثلها المتجه والأخريوازي المحور ( Y ) ويسمى بالمركبة الشاقولية ويمثله
المتجه .
وهذه تسمى عملية تحليل المتجه الى مركباته. لذلك فان المتجه المحصل يحسب من الجمع الاتجاهي للمركبتين وكما يلي: .
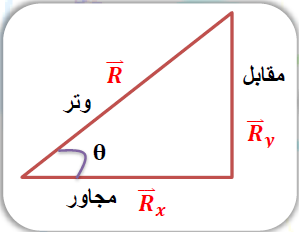
حيث ان يمثلان ضلعان قائمان في مثلث قائم الزاوية والمتجه المحصل يمثل الوتر في المثلث ويحسب مقداره طبقا لنظرية فيثاغورس كما يأتي: اما اتجاه يحدد بمعرفة الزاوية مع المحور ( x ) وذلك بتطبيق قانون الظل ( tan ) حيث ان:
يمكن ان نحسب مقدار المركبتين الافقية والشاقولية للمتجة من المعادلتين الاتيتين:
المركبة الافقية:
المركبة الشاقولية:
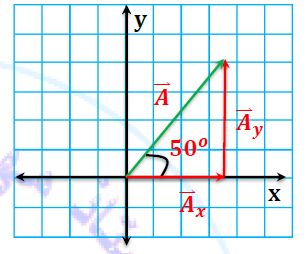
اذا كان مقدار المتجة يساوي 175m ويمثل بزاوية 50 عن المحور (x) جد مركبة المتجة .
المركبة الافقية:
المركبة الشاقولية:
ایجاد محصلة متجهين أو اكثر بطريقة التحليل المتعامد
ان عملية تحليل المتجه الى مركبتيه الافقية على المحور ( X ) والشاقولية على المحور ( Y ) يسهل جمع المتجهات من الناحية الحسابية، فيمكن جمع متجہین او اکثر مثل وذلك يتحليل كل متجه الى مركبتيه الأفقية والشاقولية اولًا، ثم تجمع المركبات الافقية لكل متجه المتجهات المركبة الأفقية المحصلة على المحور ( X ) هي:
وبالمثل تجمع المركبات الشاقولية ( المركبات على المحور Y) للمتجهات لتكون المركبة الشاقولية المحصلة على المحور ( Y ):
لايجاد محصلة متجهين او اكثر بطريقة التحليل المتعامدة تتبع الخطوات التالية:
نحلل كل متجه إلى مركبتيه الافقية والشاقولية.
تقوم بجمع المركبات الافقية لكل المتجهات فتحصل على متجه محصل موازي للمحور ( X ).
نقوم بجمع المركبات الشاقولية لكل المتجهات فنحصل على متجه محصل موازي للمحور ( Y ).
نحسب مقدار المتجه المحصل للمتجهين المتعامدين و وذلك بتطبيق نظرية فيثاغورس.
ونجد الزاوية التي يصنعها المتجه المحصل مع المحور ( X ) من العلاقة الاتية: زاوية المتجه المحصل تساوي الظل العكسي الناتج من قسمة المركبة على المركبة للمتجه المحصل .
 ملاحظة
ملاحظة
لايجاد مقدار المتجه المحصل للمتجهين و يمكننا تطبيق نظرية فيثاغورس اذا كانت الزاوية بين المتجهين و تساوي قائمة.
اما اذا كانت الزاوية بين المتجهين و لا تساوي يمكننا استعمال قانون جيب التمام ( cosine ) او قانون الجيب ( sine ) كالاتي:
قانون الجيب تمام ( cosine ):
مربع مقدارالمتجه المحصل مجموع مربعي مقداري المتجهين مطروحاً منه ضعف حاصل ضرب مقداري المتجهين مضروبا في ( cos ) الزاوية التي بينهما والمقابلة الى .
عناصر المتجة المحصل
مقدار المتجة المحصل :
اتجاه المتجة المحصل :
 ملاحظة
ملاحظة
اذا كانت الزاوية حادة اقل من نضع اشارة موجب للقانون اعلاه واذا كانت الزاوية منفرجة اكبر من واقل من نضع اشارة سالبة للقانون.
قانون الجيب ( sine ): مقدار المتجه المحصل مقسوماً على ( sine ) الزاوية التي تقابله يساوي مقدار احد المتجهين مقسوما على ( sine ) الزاوية التي تقابله.
 ملاحظات مهمة
ملاحظات مهمة
لإيجاد مقدارواتجاه المتجه المحصل للمتجهين و عندما يكون المتجهان متوازیان ( باتجاه واحد اوباتجاهين متعاكسين ) او متعامدين نستخدم العلاقات التالية:
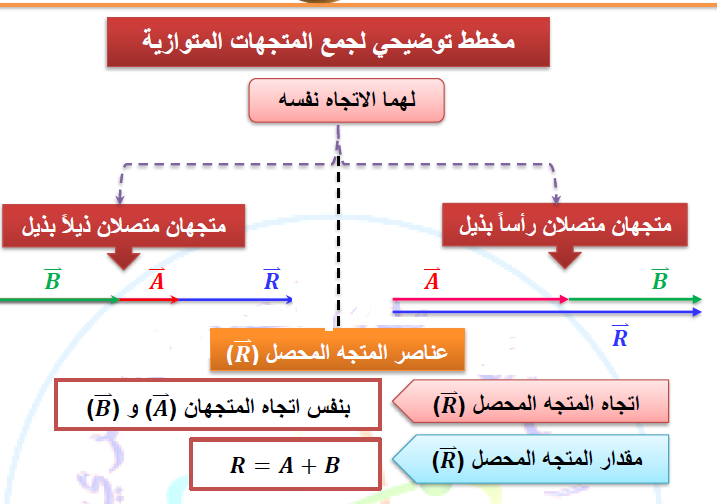
عندما يكون المتجهين بنفس الاتجاه ( متوازیان ):
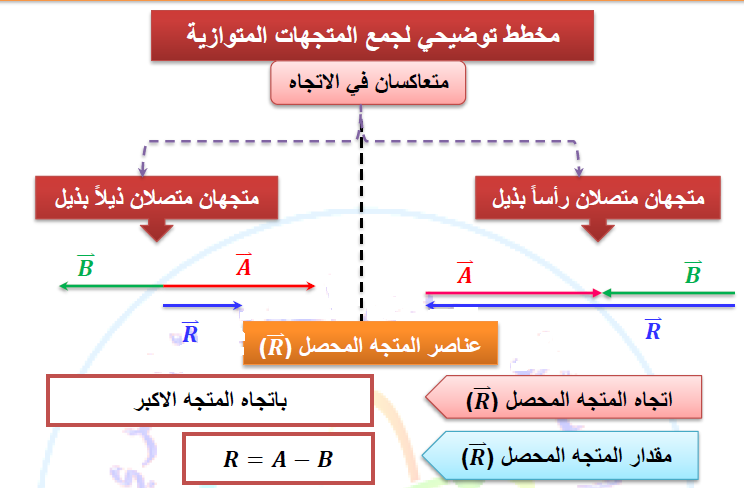
عندما يكون المتجهين متعاكسين:
عندما يكون المتجهين متعامدين:
عندما يكون المتجهين بينهما زاوية غير متعامدين:
محصلة أي متجهين باتجاه واحد هي حاصل جمع المتجهين واتجاه المتجه المحصل باتجاه المتجهيين، ومحصلة اي متجهيين متعاكسين هي طرح المتجهيين واتجاه المتجه المحصل باتجاه المتجه الاكبر.
المتجه طولة 14cm ويصنع زاوية قياسها 60 مع الاتجاه الموجب للمحور x، والمتجه طوله 20cm ويصنع زاوية قياسها 20 مع الاتجاه الموجب للمحور x حلل المتجهيين و الى مركباتهما ثم احسب مقدار واتجاه المتجة المحصل .
المركبة الافقية للمتجه :
المركبة الشاقولية للمتجه :
المركبة الافقية للمتجه :
المركبة الشاقولية للمتجه :
مقدار محصلة المركبتين الافقيتين :
مقدار محصلة المركبتين الشاقوليتين :
المتجه المحصل :
اتجاه المتجه المحصل :
تقطع سيارة مسافة 20km باتجاه الشمال ثم تقطع 35km باتجاه 60 غرب الشمال اوجد مقدار واتجاه محصلة ازاحة السيارة.
من ملاحظة الشكل فان الزاوية تساوي:
يمكن الحصول على من الشكل باستخدام قانون الجيب:
محصلة ازاحة السيارة هي وباتجاه غرب الشمال.
حلول أسئلة الصف الخامس الإعدادي
حل اسئلة رياضيات - علوم - عربي وجميع الكتب والمواد الأخرى


.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
النقاشات