فكر وأكتب
(11)- تحدٍ: بالشكل المجاور بركة محاطة بممر من البلاط عرضه 2 m.
احسب مساحة الممر.
- مساحة المربع مع الممر
- مساحة المربع بدون الممر
- مساحة الممر حول المربع هي
- مساحة نصف الدائرة مع الممر
- مساحة نصف الدائرة بدون الممر
- مساحة الممر حول نصف الدائرتين
- مساحة الممر حول البركة
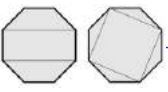
(12)- مسألة مفتوحة: الشكل يوضح طريقتان مختلفتان لإيجاد مساحة مضلع منتظم ذي ثمانية أضلاع، اشرح مضمون الطريقتين ثم ابحث عن طريقة ثالثة.
- الطريقة الأولى: مساحة المربع + أربعة أمثال مساحة المثلث.
- الطريقة الثانية: مساحة المستطيل + مثلي مساحة شبه المنحرف.
- الطريقة الثالثة: مثلثين وشبهي منحرف.
(13)- حس عددي: هل يمكن حساب مساحة دائرة بشكل تقريبي عن طريق رسم مستطيلات متجاورة داخلها ماذا يحدث عندما تجعل عدد المستطيلات المرسومة كبيراً جداً؟
- كلما كان مساحة المستطيلات كبيراً قل عددها وزاد الخطأ لذلك يفضل تصغير المساحة لأصغر ما يمكن بحيث تغطي أكبر جزء من الدائرة.
- نعم كلما زاد عدد المثلثات أمكن تغطية أكبر مساحة من الدائرة.
صيغة رياضية لحساب مساحة شكل مستوي مركب مؤلف من k من المعينات مرسومة متجاورة مع بعضها والتي طول كل من قطريها n, m من الوحدات.
مساحة المعين الواحد هي وهي متطابقة فإن:
هي المساحة.
الإثراء:
(1)- الشكل أعلاه 4 مثلثات متساوية الأضلاع ارتفاعها h=6 cm والقاعدة b=4 cm؟ اشتق قانون للمساحة ثم جد المساحة الكلية؟
لأن المثلثات متطابقة في داخل الشكل المربع، فالمساحة الكلية هي مجموع مساحة المثلثات والمربع.
(2)- في باص المدرسة أعلاه، كم شكل مستوي منتظم يظهر لديك؟ ماذا نحتاج لحساب المساحة الكلية؟
- مستطيل ومربع ونصفي دائرتين متطابقة.
- نحتاج معرفة طول وعرض المستطيل (موقع الركاب)، وطول ضلع المربع (المقدمة)، ونصف قطر الدائرة (العجلتين).

.JPG)
.JPG)
.JPG)

.JPG)
.JPG)