استعمل المعطيات وعكس المبرهنات لتبين أن $\overleftrightarrow{\mathrm{L}}//\overleftrightarrow{\mathrm{M}}$ . $\mathrm{m}\mathrm{\angle }\mathrm{x}={30}^{\circ }$ .

بما أن $\mathrm{m}\mathrm{\angle }\mathrm{x}=30°$ فإن الزاوية المقابلة لها تساوي 30 درجة وهي داخلية مع زاوية مقدارها 150 درجة، إذن مجموعهما 180 درجة، إذن زوايا متكاملة وعليه فإن $\overleftrightarrow{\mathrm{L}}//\overleftrightarrow{\mathrm{M}}$ .

تدرب وحل التمرينات

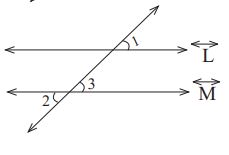
استعمل المعطيات وعكس المبرهنات لتبين أن $\overleftrightarrow{\mathrm{L}}//\overleftrightarrow{\mathrm{M}}$.

(4)- $X=7a , a=5$.

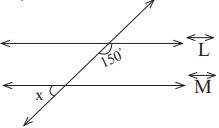
يمكن الاستفادة من حل معادلة ذات مجهول واحد باستخدام عملية الضرب، حيث أن الزاوية $x=7\times a=35°$ إذن الزاوية المجاورة لها مقدارها 145 درجة، وعليه فإن مجموع الزاويتين الداخلية هو 180 درجة وعليه فإن $\overleftrightarrow{\mathrm{L}}//\overleftrightarrow{\mathrm{M}}$.

(5)- $\mathrm{m}\mathrm{\angle }1=\mathrm{m}\mathrm{\angle }2$.

• $\mathrm{m}\mathrm{\angle }2=\mathrm{m}\mathrm{\angle }3$ بالتقابل.
• $\mathrm{m}\mathrm{\angle }1=\mathrm{m}\mathrm{\angle }3$.
• إذن $\mathrm{m}\mathrm{\angle }1=\mathrm{m}\mathrm{\angle }2$.

(6)- $\mathrm{m}\mathrm{\angle }\mathrm{x}={30}^{\circ }$.

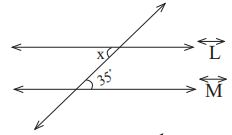
بما أن $\mathrm{m}\mathrm{\angle }\mathrm{x}=30°$ فإن الزاوية المقابلة لها تساوي 30 درجة وهي داخلية مع زاوية مقدارها 150 درجة، إذن مجموعهما 180 درجة، إذن زوايا متكاملة وعليه فإن $\overleftrightarrow{\mathrm{L}}//\overleftrightarrow{\mathrm{M}}$.