حل أسئلة مراجعة الفصل
المفردات:
- القاعدة - الارتفاع - النسبة التقريبية.
- محيط الدائرة - مساحة الدائرة - الزاويتان المتبادلتان.
- الزاويتان المتناظرتان - الزاويتان المتقابلتان بالرأس - قياس الزاوية.
- الدرجة - الشكل المستوي البسيط - الشكل المستوي المركب.
- السعة - اللتر (ل) - الملليتر (مل).
أكمل الجمل أدناه مستعملاً المفردات أعلاه:
- نسبة طول محيط الدائرة إلى طول قطرها تساوي ٣,١٤ تقريباً وتسمى النسبة التقريبية أو النسبة الثابتة.
- توجد وحدتان يمكنني استعمالهما لقياس السعة هما واللتر أو الملليتر.
- يمكنني استعمال القانون مس = نق٢ لأجد مساحة الدائرة.
- يمكنني استعمال القانون مح = ر لأجد محيط الدائرة.
- تقاس الزوايا بوحدةٍ تسمى الدرجة.
- أجد مساحة الشكل المستوي بجمع مساحات الأشكال المستوية البسيطة المكونة له.
- يمكنني إيجاد مساحة متوازي الأضلاع باستعمال القانون الآتي: حاصل ضرب طول القاعدة في الارتفاع.
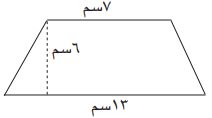
.JPG) أجد مساحة شبه المنحرف المبين في الشكل المجاور:
أجد مساحة شبه المنحرف المبين في الشكل المجاور:
- مس = × ع (ق١ + ق٢)
- مس = × ٦ (٧ + ١٣)
- مس = ٦٠ سم مربع.
.JPG) أجد محيط دائرةٍ نصف قطرها ٨ سم.
أجد محيط دائرةٍ نصف قطرها ٨ سم.
- القطر = نصف القطر × ٢
- القطر = ٨ × ٢ = ١٦ سم.
- مح = ر ×
- مح = ١٦ × ٣,١٤
- مح = ٥٠,٢٤ سم.
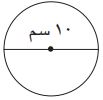
.JPG) أجد مساحة الدائرة المبينة في الشكل المجاور:
أجد مساحة الدائرة المبينة في الشكل المجاور:
- مس = نق٢ ×
- مس = ٣,١٤ × ٥ × ٥
- مس = ٣,١٤ × ٢٥
- مس = ٧٨,٥٠ م مربع.
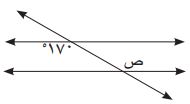
.JPG) أجد القياس ص في الشكل المجاور.
أجد القياس ص في الشكل المجاور.
قياس الزاوية ص = ١٧٠ درجة (زاويتان متبادلتان ومتساويتان بالقياس).
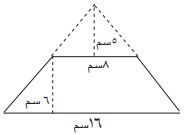
.JPG) أجد مساحة الشكل المستوي المركب المجاور:
أجد مساحة الشكل المستوي المركب المجاور:
- مساحة المثلث = نصف القاعدة × الارتفاع.
- مساحة المثلث = × ٨ × ٥
- مس = × ٤٠ = ٢٠ سم مربع.
- مساحة شبه المنحرف = × ع (ق١ + ق٢).
- مس = × ٦ × (٨ + ١٦).
- مس = × ٦ × ٢٤ = ٧٢ سم مربع.
- مساحة الشكل المستوي المركب = مساحة المثلث + مساحة شبه المنحرف.
- مساحة الشكل المستوي المركب = ٢٠ + ٧٢
- مساحة الشكل المستوي المركب = ٩٢ سم مربع.
.JPG) تتسع علبة ٨٠٠٠ ملليتر من مادةٍ معقمةٍ، أعبر عن هذا المقدار بالملليترات.
تتسع علبة ٨٠٠٠ ملليتر من مادةٍ معقمةٍ، أعبر عن هذا المقدار بالملليترات.
١ ل = ١٠٠٠ مل.
٨٠٠٠ ÷ ١٠٠٠ = ٨ ل.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)