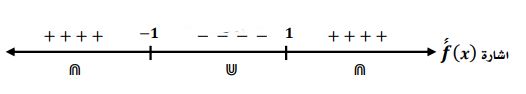حلول الأسئلة
السؤال
ارسم باستخدام معلوماتك في التفاضل الدوال الآتية:
الحل
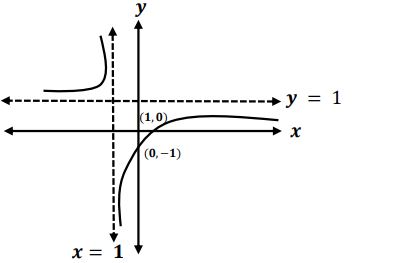
- أوسع مجال للدالة =
- التقاطع مع المحورين:
لأن غير معرفة لا توجد نقاط تقاطع مع محور الصادات.
لأن لا توجد نقاط تقاطع مع محور السينات.
- التناظر: التناظر مع نقطة الأصل.
-
المحاذيات:
- المستقيم المحاذي الشاقولي
- المستقيم المحاذي الأفقي
- مناطق التزايد والتناقص.
توجد فجوة ولا توجد نقاط حرجة.
الدالة متناقصة بالفترتين
لا توجد نقاط انقلاب.
- محدبة
- مقعرة
الرسم البياني:
| 2 | 1 | 0 | 1- | 2- | |
| 1 | فجوة | 1- | |||
مشاركة الحل
تمارين (5-3)
ارسم باستخدام معلوماتك في التفاضل الدوال الآتية:
- أوسع مجال للدالة = R
- نقاط التقاطع مع المحورين:
نقط التقاطع
-
التناظر: لا يوجد تناظر مع محور الصادات أو نقطة الأصل.
-
المحاذيات: لا يوجد مستقيمات محاذية لأن الدالة غير نسبية.
-
مناطق التزايد والتناقص.
النقطة نقطة نهاية عظمى محلية.
- متزايدة
- متناقصة
- الدالة محدبة دائماً مهما تكن قيمة ولا توجد نقطة انقلاب.
الرسم البياني:
| 0 | 5- | 2 | ||
| 10 | 0 | 0 | ||
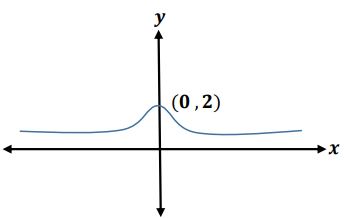
- أوسع مجال للدالة = R
- نقاط التقاطع مع المحورين:
فإن
نقط التقاطع
-
التناظر:
لا يوجد تناظر مع محور الصادات أو نقطة الأصل.
-
المحاذيات: لا يوجد مستقيمات محاذية لأن الدالة ليست نسبية.
-
مناطق التزايد والتناقص.
نقطة نهاية صغرى محلية.
- متزايدة
- متناقصة
- مناطق التقعر والتحدب.
الدالة مقعرة ولا توجد نقطة انقلاب
الرسم البياني:
| 1 | 0 | 1- | 2- | 3- | |
| 8 | 3 | 0 | 1- | 0 | |
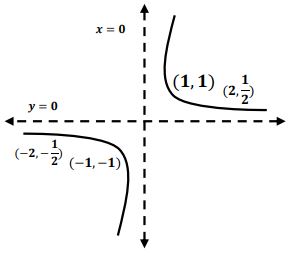
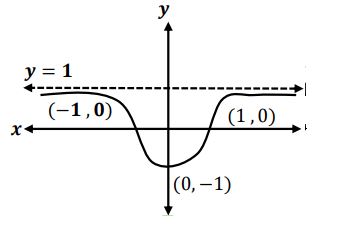
- أوسع مجال للدالة = R
- نقاط التقاطع مع المحورين:
- التناظر:
لا يوجد تناظر مع محور الصادات أو نقطة الأصل
-
المحاذيات: لا يوجد مستقيمات محاذية لأن الدالة غير نسبية.
-
مناطق التزايد والتناقص.
نقطة حرجة
متناقصة
نقطة انقلاب مرشحة
- مقعرة
- محدبة
الرسم البياني:
| 1- | 1 | 0 | 2 | |
| 9 | 1 | 2 | 0 | |
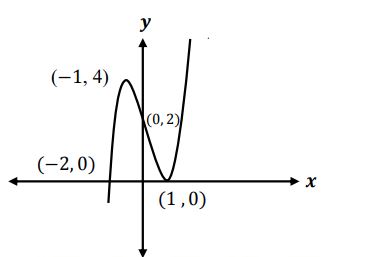
- أوسع مجال للدالة = R
- نقاط التقاطع مع المحورين:
نقط التقاطع
- التناظر: لا يوجد تناظر مع محور الصادات أو نقطة الأصل.
الدالة متناظرة حول نقطة الأصل ولا يوجد تناظر حول محور الصادات.
-
المحاذيات: لا يوجد مستقيمات محاذية لأن الدالة غير نسبية.
-
مناطق التزايد والتناقص.
- نقطة نهاية عظمى
- نقطة نهاية صغرى
- متزايدة في
- متناقصة في
نقطة انقلاب.
- مقعرة
- محدبة
الرسم البياني:
| 0 | |||||
| 0 | 0 | 0 | |||
ملاحظة: التحدب بقدر التقعر في الرسم لأن التناظر حول نقطة الأصل.
- أوسع مجال للدالة =
- التقاطع مع المحورين:
لأن غير معرفة لا توجد نقاط تقاطع مع محور الصادات.
لأن لا توجد نقاط تقاطع مع محور السينات.
- التناظر: التناظر مع نقطة الأصل.
-
المحاذيات:
- المستقيم المحاذي الشاقولي
- المستقيم المحاذي الأفقي
- مناطق التزايد والتناقص.
توجد فجوة ولا توجد نقاط حرجة.
الدالة متناقصة بالفترتين
لا توجد نقاط انقلاب.
- محدبة
- مقعرة
الرسم البياني:
| 2 | 1 | 0 | 1- | 2- | |
| 1 | فجوة | 1- | |||
- أوسع مجال للدالة =
- التقاطع مع المحورين:
- التناظر: لا يوجد تناظر مع محور الصادات أو نقطة الأصل لأن:
-
المحاذيات:
- المحاذي الشاقولي
- المحاذي الأفقي
- مناطق التزايد والتناقص.
لا توجد نقاط حرجة.
تزايد
- محدبة في
- مقعرة في
الرسم البياني:
| 2- | 2 | 1 | 0 | |
| 3 | 0 | 1- | ||
- أوسع مجال للدالة =
- التقاطع مع المحورين:
- التناظر: لا يوجد تناظر مع محور الصادات أو نقطة الأصل.
-
المحاذيات: لا يوجد مستقيمات محاذية لأن الدالة ليست نسبية.
- مناطق التزايد والتناقص.
- نقطة حرجة وتمثل نهاية صغرى.
- نقطة حرجة وتمثل نهاية عظمى.
- متزايدة في
- متناقصة في الفترة المفتوحة
نقطة انقلاب.
- محدبة في
- مقعرة في
الرسم البياني:
| 1- | 2- | 1 | 0 | |
| 4 | 0 | 0 | 2 | |
- أوسع مجال للدالة = لأن
- التقاطع مع المحورين:
- التناظر: التناظر حول محور الصادات لأن
- المحاذيات:
لا يوجد مستقيم شاقولي
المحاذي الأفقي
- مناطق التزايد والتناقص.
نقطة نهاية صغرى
- متزايدة في
- متناقصة في
محدبة في
مقعرة في
الرسم البياني:
|
|
0 | 1 | 1- | ||
| 1- | 0 | 0 | |||
- أوسع مجال للدالة =
- التقاطع مع المحورين:
- التناظر: التناظر حول محور الصادات لأن
- المحاذيات: لا يوجد مستقيمات محاذية لأن الدالة ليست نسبية.
- مناطق التزايد والتناقص.
- نقطة نهاية عظمى محلية.
- نقطة نهاية عظمى محلية.
- نقطة نهاية صغرى.
- متزايدة في والفترة
- متناقصة في والفترة
النقط نقط انقلاب مرشحة.
مقعرة في
محدبة في
الرسم البياني:
|
|
1- | 1 | 0 | |||
| 1 | 1 | 0 | 0 | |||
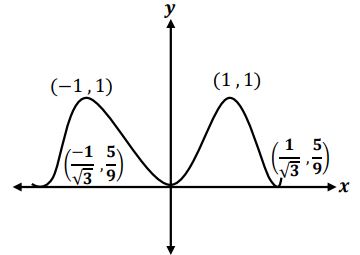
- أوسع مجال للدالة = لأن
- نقاط التقاطع مع المحورين:
- التناظر: التناظر حول محور الصادات لأن
- المحاذيات:
لا يوجد مستقيم شاقولي
المحاذي الأفقي
- مناطق التزايد والتناقص.
النقطة نقطة نهاية عظمى محلية.
- متزايدة بالفترة
- متناقصة بالفترة
النقاط نقاط انقلاب.
- مقعرة في
- محدبة في الفترة
الرسم البياني:
| 0 | 1 | 1- | |
| 2 | |||

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

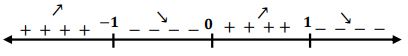
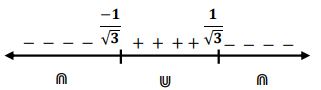
.JPG)