حلول الأسئلة
السؤال
ارسم منحني الدالة باستخدام بمعلوماتك في التفاضل
الحل
- أوسع مجال للدالة =
- نقاط التقاطع مع المحورين.
1. المحور السيني:
2. المحور الصادي:
- التناظر: الدالة متناظرة مع نقطة الأصل لأن:
-
المحاذيات: لا يوجد محاذيات لأن الدالة ليست نسبية.
-
مناطق التزايد والتناقص.
لا توجد نقاط نهايات والدالة متزايدة في
نقطة حرجة لا تمثل نقطة نهاية.
- مناطق التحدب والتقعر.
مناطق الانقلاب
- الدالة محدبة في
- الدالة مقعرة في
الرسم البياني:
| 0 | 0 | |
| 1 | 1 | |
| 1- | 1- | |
| 2 | 32 |
مشاركة الحل
رسم المخطط البياني للدالة
لرسم المخطط البياني لأي دالة معطاة نتبع الخطوات التالية والتي تمثل النقط الأساسية للرسم:
- أوسع مجال للدالة.
- نقط التقاطع مع المحورين.
- التناظر.
- المحاذيات.
- دراسة وما ينتج عنها.
- دراسة وما ينتج عنها.
- تحديد النقط الخاصة بالرسم ومن ثم رسمها.
1. أوسع مجال للدالة.
- كثيرات الحدود: أوسع مجال لها =
- الدوال الكسرية: القيم التي تجعل المقام = صفر /
- الدوال الجذرية:
2. نقط التقاطع مع المحورين: وهي على نوعين:
- التقاطع مع المحور الصادي: لإيجاد نقط التقاطع مع المحور نجعل لإيجاد قيم
- التقاطع مع المحور السيني: لإيجاد نقط التقاطع مع المحور نجعل لإيجاد قيم
مثال توضيحي:
جد نقاط التقاطع:
نقط التقاطع
3. التناظر: هو على نوعين:
- يكون المنحني متناظر مع المحور الصادي إذا كانت أسس المتغير كلها زوجية أي أن
- يكون المنحني متناظر حول نقطة الأصل إذا كانت أسس المتغير كلها فردية أي أن
مثال توضيحي:
4. المحاذيات: دراستنا للمحاذيات تقتصر على الدوال الكسرية فقط:
- المحاذي الأفقي الموازي لمحور السينات: تكون معادلته هذا العدد هو حاصل قسمة معامل الحد الأكبر درجة من البسط على معامل الحد الأكبر درجة من المقام بشرط تساوي الدرجتين.
- المحاذي الشاقولي (العمودي) الموازي لمحور الصادات: نجعل الدالة بدلالة المتغير أي نجعل ثم نجعل ونجد قيم فهي تمثل معادلة المستقيم الشاقولي.
(1)- ارسم بالاستعانة بمعلوماتك في التفاضل منحني الدالة
- أوسع مجال للدالة =
- نقاط التقاطع مع المحورين.
1. المحور السيني:
2. المحور الصادي:
-
التناظر: الدالة متناظرة مع المحور الصادي لأنه
-
المحاذيات: لا يوجد محاذيات.
-
مناطق التزايد والتناقص.
- مناطق التناقص
- مناطق التزايد
- مناطق التحدب والتقعر.
- مناطق الانقلاب
- مناطق التحدب
- مناطق التقعر
الرسم البياني:
| 0 | 1 | |
| 0 | 1- | |
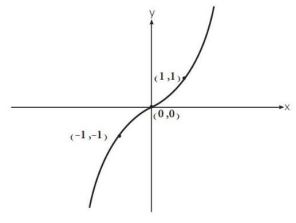
(2)- ارسم منحني الدالة باستخدام بمعلوماتك في التفاضل
- أوسع مجال للدالة =
- نقاط التقاطع مع المحورين.
1. المحور السيني:
2. المحور الصادي:
- التناظر: الدالة متناظرة مع نقطة الأصل لأن:
-
المحاذيات: لا يوجد محاذيات لأن الدالة ليست نسبية.
-
مناطق التزايد والتناقص.
لا توجد نقاط نهايات والدالة متزايدة في
نقطة حرجة لا تمثل نقطة نهاية.
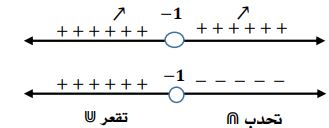
- مناطق التحدب والتقعر.
مناطق الانقلاب
- الدالة محدبة في
- الدالة مقعرة في
الرسم البياني:
| 0 | 0 | |
| 1 | 1 | |
| 1- | 1- | |
| 2 | 32 |
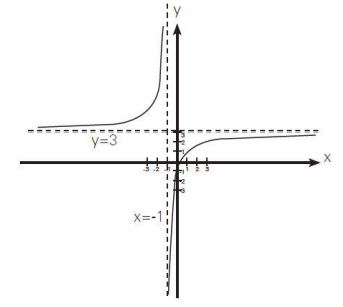
(3)- بالاستعانة بالتفاضل ارسم منحني الدالة
- أوسع مجال للدالة =
- نقاط التقاطع مع المحورين.
1. المحور السيني:
2. المحور الصادي:
- التناظر: العدد ينتمي إلى مجال الدالة لا ينتمي إلى الدالة لذلك فالمنحني غير متناظر مع محور الصادات وغير متناظر مع نقطة الأصل.
- المحاذيات:
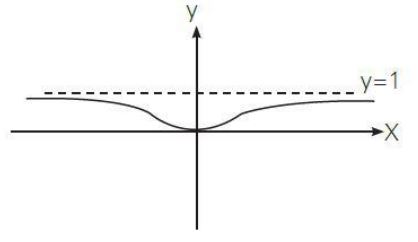
الدالة متزايدة في ولا توجد نقاط حرجة.
- الدالة مقعرة في
- الدالة محدبة في
الدالة لا تملك نقطة انقلاب لأن لا ينتمي إلى مجال الدالة.
الرسم البياني:
| 1- | 0 | |
| 0 | ||
| 1- | 1- | |
| 2 | ||
| 7 | 2- | |
| 1 | 1 |
(4)- باستخدام معلوماتك في التفاضل ارسم المنحني
- أوسع مجال للدالة =
- نقاط التقاطع مع المحورين.
1. المحور السينات:
مع محور السينات.
2. المحور الصادات:
مع محور الصادات.
التناظر مع الصادي:
متناظرة مع المحور الصادي لأنها زوجية.
المحاذيات:
لا يوجد محاذي عمودي
مناطق التزايد والتناقص.
نقطة نهاية صغرى محلية.
- تزايد
- تناقص
محدبة في
مقعرة في الفترة المفتوحة
نقطتا الانقلاب
الرسم البياني:
| 0 | 0 | |
| 1- | ||
| 2 | ||
| 2- | ||
| 1 |
(5)- ارسم بالاستعانة بمعلوماتك في التفاضل الدالة
- أوسع مجال للدالة =
- نقاط التقاطع مع المحورين.
نقطة التقاطع مع المحور الصادي.
التناظر:
لا يوجد تناظر مع محور الصادات أو نقطة الأصل لأن:
- المحاذيات: لا يوجد محاذيات لأن الدالة ليست نسبية.
- مناطق التزايد والتناقص.
- متزايدة في كل من
- متناقصة في الفترة
- نقطة نهاية عظمى محلية.
- نقطة نهاية عظمى محلية.
مناطق التقعر والتحدب.
- مقعرة في
- محدبة في
نقطة الانقلاب
الرسم البياني:
| 4 | 0 | |
| 2 | 1 | |
| 0 | 2 | |
| 4 | 3 | |
| 0 | 1- |

.JPG)
.JPG)
.JPG)
.JPG)
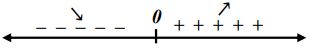
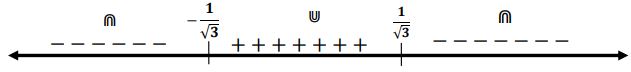
.JPG)
.JPG)
.JPG)