جد معادلة القطع المكافئ إذا علمت أن:

بؤرته هي $(0,5)$ ورأسه في نقطة الأصل.

البؤرة:

$\because (0,p)=(0,5)$

المعادلة القياسية للقطع المكافئ:

$\therefore p=5\Rightarrow x^2=4py$

معادلة القطع المكافئ:

$\therefore x^2=4\left(5\right)x\Rightarrow x^2=20y$

القطع المكافئ

القطع المكافئ: هو مجموعة النقط $M(x,y)$ في المستوى والتي يكون بعدها عن نقطة ثابتة $\mathrm{F}(\mathrm{p},0)$ تسمى البؤرة حيث $p\ne 0$ يساوي بعدها عن مستقيم معلوم يسمى (الدليل $D$) وهو لا يحتوي البؤرة.

أو بمعنى آخر هو مجموعة من النقط داخل مستوي والتي يكون بعدها عن نقطة معلومة مساوياً لبعدها عن مستقيم معلوم.

للقطع المكافئ حالتان هما:

أولاً: البؤرة تقع على المحور السيني (x-axis) والرأس في نقطة الأصل.

1- الفتحة نحو اليمين:

قانون البعد:

$\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$

تعريف القطع المكافئ:

$\frac{MF}{MQ}=e=1\Rightarrow MF=MQ$

بتربيع الطرفين:

$\begin{array}{rl}& \sqrt{(x-p{)}^2+(y-0{)}^2}=\sqrt{(x+p{)}^2+(y-y{)}^2}\\ & x^2-2px+P^2+y^2=x^2+2px+P^2\end{array}$

معادلة القطع المكافئ:

$\therefore y^2=4px ,\hspace{0.17em}\mathrm{\forall }p>0$

معادلة الدليل:

$x=-p$

2- الفتحة نحو اليسار:

معادلة القطع المكافئ:

$y^2=-4px$

معادلة الدليل:

$x=p$

ثانياً: البؤرة تقع على المحور الصادات (y-axis) والرأس في نقطة الأصل.

1- الفتحة نحو الأعلى:

تكون هنا معادلة القطع حقيقية.

قانون البعد:

$\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$

تعريف القطع المكافئ:

$MF=MQ$

بتربيع الطرفين:

$\begin{array}{rl}& \sqrt{(x-0{)}^2+(y-p{)}^2}=\sqrt{(x-x{)}^2+(y+p{)}^2}\\ & x^2+y^2-2py+P^2=y^2+2py+P^2\end{array}$

معادلة القطع المكافئ:

$x^2=4py , \mathrm{\forall }p>0$

معادلة الدليل:

$y=-p$

2- الفتحة نحو الأسفل:

معادلة القطع المكافئ:

$x^2=-4py$

معادلة الدليل:

$y=p$

نلاحظ مما سبق أنه يوجد معادلتين للقطع المكافئ الذي راسه نقطة الاصل (0,0) إحداهما عندما يكون على المحور السيني والأخرى عندما يكون على المحور الصادي والجدول أدناه يوضح ذلك:

ملاحظات عامة:

1. إشارة البؤرة عكس إشارة الدليل والعكس صحيح.
2. المسافة بين البؤرة والدليل =$2p$.
3. كل نقطة تنتمي للقطع المكافئ فهي تحقق معادلته (أي أن القطع المكافئ يمر بها).
4. كل نقطة تنتمي للقطع المكافئ بعدها عن البؤرة يساوي بعدها عن الدليل.
5. رأس القطع المكافئ هو نقطة الأصل ومعادلة المميز الخاصة به هي $b^2-4ac=0$..

جدول تظهر فيه جميع حالات القطع المكافئ:

(1)- جد البؤرة ومعادلة الدليل للقطع المكافئ في كل مما ياتي:

$y^2=-8x$

$\begin{array}{rl}& y^2=-8x\\ & y^2=-4px\end{array}$

بالمقارنة مع المعادلة القياسية:

$4p=8\Rightarrow p=\frac{8}{4}=2$

البؤرة:

$F(-p,0)=F(-2,0)$

معادلة الدليل:

$x=p\Rightarrow x=2$

$y^2=4x$

$$\begin{gathered} \because y^2=4px \\ 4p=4\Rightarrow p=\frac{4}{4}=1 \end{gathered}$$

البؤرة:

$F(p,0)=F(1,0)$

معادلة الدليل:

$x=-p\Rightarrow x=-1$

$y^2=4px\Rightarrow y^2=4\left(1\right)x=4x\Rightarrow y=\pm 2\sqrt{x}$

ملاحظات لإيجاد معادلة القطع المكافئ رأسه نقطة الأصل ضمن الحالات الرئيسية الآتية:

• أولاً: إذا علمت بؤرة القطع المكافئ فإن الحل يكون بشكل مباشر تستخرج قيمة $p$ ونكتب المعادلة ونعوض.
• ثانياً: إذا علمت معادلة الدليل فإن البؤرة ستكون على نفس المحور الذي يقطعه الدليل بالاتجاه الآخر فنقوم باستخراج إحداثي البؤرة ثم نستخرج قيمة $p$ ونكتب المعادلة ونعوض.

(2)- جد معادلة القطع المكافئ إذا علمت أن:

بؤرته هي $(3,0)$ ورأسه في نقطة الأصل.

البؤرة:

$\because (p,0)=(3,0)$

المعادلة القياسية للقطع المكافئ:

$\therefore p=3\Rightarrow y^2=4px$

معادلة القطع المكافئ:

$\therefore y^2=4\left(3\right)x\Rightarrow y^2=12x$

معادلة الدليل $2x-6=0$ ورأسه في نقطة الأصل.

معادلة الدليل:

$\begin{array}{rl}& \because 2x-6=0\\ & \therefore 2x=6\Rightarrow x=3\end{array}$

المعادلة القياسية للقطع المكافئ:

$\therefore p=3\Rightarrow y^2=-4px$

معادلة القطع المكافئ:

$\therefore y^2=-4\left(3\right)x\Rightarrow y^2=-12x$

(3)- جد معادلة القطع المكافئ إذا علمت أن:

بؤرته هي $(0,5)$ ورأسه في نقطة الأصل.

البؤرة:

$\because (0,p)=(0,5)$

المعادلة القياسية للقطع المكافئ:

$\therefore p=5\Rightarrow x^2=4py$

معادلة القطع المكافئ:

$\therefore x^2=4\left(5\right)x\Rightarrow x^2=20y$

معادلة الدليل $y=7$ ورأسه في نقطة الأصل.

بالمقارنة مع معادلة الدليل:

$\because y=7$

المعادلة القياسية للقطع المكافئ:

$\therefore p=7\Rightarrow x^2=-4py$

معادلة القطع المكافئ:

$x^2=-4\left(7\right)y\Rightarrow x^2=-28y$

ثالثاً: إذا مر القطع المكافئ بنقطة معينة فإنها تحقق معادلته فإذا كانت البؤرة تنتمي إلى محور السينات تكتب إحدى معادلتي محور السينات ثم التعويض بها لاستخراج قيمة $p$ ثم إعادة تعويضها بمعادلة القطع المكافئ وإذا كانت البؤرة تنتمي لمحور الصادات كذلك نكتب إحدى معادلتي محور الصادات ثم التعويض بها لاستخراج قيمة $p$ ثم إعادة تعويضها بمعادلة القطع المكافئ وفي حالة لم يحدد موقع البؤرة يتم أخذ احتمالان معاً.

(4)- جد معادلة القطع المكافئ الذي بؤرته تنتمي لمحور السينات ورأسه نقطة الأصل ويمر بالنقطة $(2,4)$

بما أن النقطة تقع بالربع الأول والبؤرة تقع على محور السينات فإن البؤرة تقع على محور السينات الموجب فتكون المعادلة:

$$\begin{gathered} y^2=4px\Rightarrow (4{)}^2=4p(2)\Rightarrow 16=8p\Rightarrow p=\frac{16}{8}=2 \\ \therefore y^2=8x \end{gathered}$$

(5)- جد معادلة القطع المكافئ الذي رأسه نقطة الأصل وبؤرته تقع على محور الصادات ويمر بالنقطة $(-1,-4)$

بما أن النقطة تقع بالربع الثالث والبؤرة تقع على محور الصادات فإن البؤرة تقع على محور الصادات السالب فتكون المعادلة:

$$\begin{gathered} x^2=-4py\Rightarrow (-1{)}^2=-4p(-4)\Rightarrow 1=16p\Rightarrow p=\frac{1}{16} \\ \therefore x^2=-\frac{1}{4}y \end{gathered}$$

(6)- جد معادلة القطع المكافئ الذي رأسه نقطة الأصل ويمر بالنقطة $(-2,6)$

يوجد احتمالين للمعادلة القياسية للقطع المكافئ لعدم تحديد البؤرة، والاحتمالين هما:

رابعاً: إذا مر القطع المكافئ بنقطتين تقعان في ربعين متجاورين فإن البؤرة تقع على محور تناظر الربعين فنقوم بكتابة المعادلة المناسبة ثم نقوم بتعويض أي نقطة من النقطتين لاستخراج قيمة $p$ ثم إعادة تعويضها بمعادلة القطع.

(7)- جد معادلة القطع المكافئ الذي يمر بالنقطتين $(2,-4) , (2,4)$ ورأسه نقطة الأصل.

النقطتان تقعان بالربعين الأول والرابع فهذا يعني أن البؤرة تقع على محور السينات الموجب وبالتالي تكون معادلة القطع المكافئ هي:

$\begin{array}{rl}& y^2=4px\Rightarrow (4{)}^2=4p(2)\Rightarrow 16=8p\Rightarrow p=\frac{16}{8}=2\\ & y^2=4px\Rightarrow y^2=4\left(2\right)x\Rightarrow y^2=8x\end{array}$

(8)- جد معادلة القطع المكافئ الذي مركزه نقطة الأصل ويمر بالنقطتين $(-2\sqrt{3},-1) , (\sqrt{6},-\frac{1}{2})$

بما أن النقطتين تقعان في الربعين الثالث والرابع فإن البؤرة تقع على محور الصادات السالب وبذلك تكون معادلة القطع المكافئ هي:

$\begin{array}{rl}& x^2=-4py\Rightarrow (\sqrt{6}{)}^2=-4p(-\frac{1}{2})\Rightarrow 6=2p\Rightarrow p=3\\ & x^2=-4py\Rightarrow x^2=-4\left(3\right)y\Rightarrow x^2=-12y\end{array}$

(10)- جد معادلة القطع المكافئ الذي يمر بالنقطتين $(-4,-1) , (4,-1)$ والرأس في نقطة الأصل.

بما أن النقطتين تقعان في الربعين الثالث والرابع فإن البؤرة تقع على محور الصادات السالب وبذلك تكون معادلة القطع المكافئ هي:

$\begin{array}{rl}& x^2=-4py\\ & (-4{)}^2=-4p(-1)\Rightarrow 16=-4p(-1)\Rightarrow 16=4p\Rightarrow p=\frac{16}{4}=4\\ & x^2=-4\left(4\right)y\Rightarrow x^2=-16y\end{array}$

خامساً: إذا مر دليل القطع المكافئ بنقطة معينة $(a,b)$ فإذا كانت البؤرة تقع على محور السينات فإن معادلة الدليل هي $x=a$ فنقوم باستخراج إحداثي البؤرة ثم نستخرج قيمة $p$ ثم نكتب المعادلة المناسبة ثم التعويض بها، وإذا كانت البؤرة تنتمي لمحور الصادات فإن معادلة الدليل هي $y=b$ فنقوم باستخراج إحداثي البؤرة ثم نستخرج قيمة $p$ ونكتب المعادلة المناسبة وتعوض بها وفي حالة عدم تحديد موقع البؤرة فيتم أخذ احتمالان معاً.

(10)- جد معادلة القطع المكافئ الذي رأسه نقطة الأصل وبؤرته تنتمي لمحور السينات ودليله يمر بالنقطة $(-2,3)$

بما أن محور القطع المكافئ هو محور السينات والدليل يمر بنقطة تقع في الربع الثاني فإن البؤرة تقع على المحور السيني الموجب وبالتالي تكون:

معادلة الدليل $x=-2$

$y=-4\Rightarrow F(0,4)\Rightarrow p=4\Rightarrow x^2=4py\Rightarrow x^2=\left(4\right)\left(4\right)y\Rightarrow x^2=16y$

(11)- جد معادلة القطع المكافئ الذي رأسه نقطة الأصل وبؤرته تنتمي لمحور الصادات ودليله يمر بالنقطة $(3,-5)$

يوجد احتمالين للمعادلة القياسية للقطع المكافئ لعدم تحديد البؤرة، والاحتمالين هما:

سادساً: إذا مر الدليل بنقطتين مختلفتين فإن معادلة الدليل هي $\text{either }(x=) \text{or }(y=)$ المسقط المتساوي من النقطتين فنقوم باستخراج إحداثي قيمة $p$ ثم نكتب المعادلة المناسبة ثم التعويض بها.

(12)- جد معادلة القطع المكافئ في الحالات التالية:

دليله يمر بالنقطتين $(-3,9) , (-3,1)$ ورأسه نقطة الأصل:

معادلة الدليل هي $x=-3$ أي أن $p=3$

$F(3,0)\Rightarrow y^2=4px\Rightarrow y^2=4\left(3\right)x\Rightarrow y^2=12x$

دليله يمر بالنقطتين $(-7,2) , (-4,2)$ ورأسه نقطة الأصل:

معادلة الدليل هي $y=2$ أي أن $p=2$

$F(0,-2)\Rightarrow x^2=-4py\Rightarrow x^2=-4\left(2\right)x\Rightarrow x^2=-8y$

سابعاً: إذا مر الدليل بنقطة تقع على أحد المحورين الإحداثيين فإن البؤرة تقع على نفس المحور بالاتجاه الآخر.

(13)- جد معادلة القطع المكافئ في الحالات الآتية:

دليله يمر بالنقطتين $(-4,0)$ ورأسه نقطة الأصل:

بما أن الدليل يمر بالنقطة $(-4,0)$ فهذا يعني أن البؤرة $(4,0)$ أي أن $p=4$

$y^2=4px⟹y^2=4\left(4\right)x\Rightarrow y^2=16x$

دليله يمر بنقطة تقاطع $2x+3y=12$ مع محور الصادات ورأسه نقطة الأصل:

$\begin{array}{rl}& x=0\Rightarrow 2\left(0\right)+3y=12\Rightarrow 3y=12\Rightarrow y=4\\ & F(0,-4)\Rightarrow p=4\Rightarrow x^2=-4py\Rightarrow x^2=-4\left(4\right)y\Rightarrow x^2=-16y\end{array}$

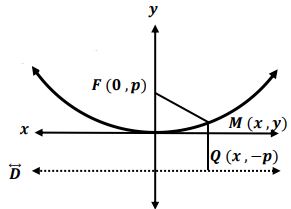
(14)- باستخدام التعريف جد معادلة القطع المكافئ إذا علمت أن بؤرته $(\sqrt{3},0)$ ورأسه في نقطة الأصل.

البؤرة $F(\sqrt{3},0)$ ولتكن النقطة $M(x,y)$ تنتمي إلى منحني القطع المكافئ ولتكن النقطة $Q(-\sqrt{3},y)$ هي نقطة تقاطع العمود المرسوم من $M$ على الدليل $\overleftrightarrow{\mathrm{D}}$ فمن تعريف القطع المكافئ $MF=MQ$

تكون معادلة القطع المكافئ هي:

$\begin{array}{rl}& \sqrt{(x-\sqrt{3}{)}^2+(y-0{)}^2}=\sqrt{(x+\sqrt{3}{)}^2+(y-y{)}^2}\\ & (x-\sqrt{3}{)}^2+(y{)}^2=(x+\sqrt{3}{)}^2\\ & x^2-2\sqrt{3}x+3+y^2=x^2+2\sqrt{3}x+3\\ & y^2=4\sqrt{3}x\end{array}$

(15)- جد البؤرة ومعادلة الدليل للقطع المكافئ $3x^2-24y=0$

نقسم طرفي المعادلة على 3:

$\begin{array}{rl}& \because 3x^2-24y=0\Rightarrow 3x^2=24y\\ & x^2=8y\end{array}$

بالمقارنة مع المعادلة القياسية:

$\begin{array}{rl}& x^2=4py\\ & 4p=8\Rightarrow p=\frac{8}{4}=2\end{array}$

البؤرة:

$F(0,p)=F(0,2)$

معادلة الدليل:

$y=-p\Rightarrow y=-2$

(16)- جد البؤرة ومعادلة الدليل للقطع المكافئ $3y^2=16x-y^2$

$3y^2+y^2=16x$

نقسم على 4:

$\begin{array}{rl}& 4y^2=16x\\ & y^2=4x\\ & y^2=4px\Rightarrow 4p=4\Rightarrow p=\frac{4}{4}=1\end{array}$

البؤرة:

$F(1,0)$

معادلة الدليل:

$x=-1$

(17)- إذا كانت $x^2-2ky=0$ تمثل معادلة قطع مكافئ بؤرته $(0,1)$ فجد قيمة $\left(k\right)$

البؤرة $(0,1)$ صادية موجبة فتكون معادلة القطع هي $x^2=4py$

$\begin{array}{rl}& p=1\Rightarrow x^2=4y\\ & x^2=4y\\ & x^2=2ky\\ & 2k=4\Rightarrow k=2\end{array}$

(18)- جد قيمة $a$ من معادلة القطع المكافئ $\frac{1}{4}{y}^2=ax$ رأسه نقطة الأصل ويمر دليله بالنقطة $(-6,3)$

معادلة قطع مكافئ بؤرته تقع على محور السينات:

$\frac{1}{4}{y}^2=ax\Rightarrow y^2=4ax$

الدليل يمر بالنقطة $(-6,3)$ فتكون معادلة الدليل:

$x=-6\Rightarrow p=6$

$\begin{array}{rl}& y^2=4px\\ & y^2=4ax\\ & 4a=4p\Rightarrow a=p\Rightarrow a=6\end{array}$

ملاحظات:

1. إذا كان القطع المكافئ يمر بالنقطتين المتساويتين $(x_1,-y_1) , (x_1,y_1)$ فالبؤرة سينية.
2. إذا كان القطع المكافئ يمر بالنقطتين المتساويتين $(-x_1,y_1) , (x_1,y_1)$ فالبؤرة صادية.