حلول الأسئلة
السؤال
أكمل الجمل أدناه مستعملاً المفردات أعلاه:
- الزاوية الداخلية - الزاوية الخارجية - الزاويتان المتجاورتان.
- الزاويتان المتقابلتان بالرأس - الزاويتان المتناظرتان - الزاويتان المتبادلتان.
- الزاويتان المتتامتان - الزاويتان المتكاملتان - تنصيف الزاوية.
- الدائرة - مركز الدائرة - وتر الدائرة - قطر الدائرة - نصف قطر الدائرة.
الحل
- الزاويتان المتجاورتان هما زاويتان بينهما ضلعٌ مشتركٌ وضلعاهما الآخران في جهتين مختلفتين من الضلع المشترك.
- الدائرة هي مجموعةٌ من النقاط المتصلة في المستوى التي لها البعد نفسه عن نقطةٍ ثابتةٍ تسمى مركز الدائرة.
- القطعة المستقيمة التي طرفاها على الدائرة تسمى وتر الدائرة.
- الوتر الذي يمر بمركز الدائرة يسمى قطر الدائرة.
- القطعة المستقيمة التي تصل بين مركز الدائرة ونقطة على الدائرة تسمى نصف قطر الدائرة.
- الزاويتان المتقابلتان هما زاويتان مشتركتان في الرأس وغير متجاورتين.
- الزاويتان المتبادلتان هما الزاويتان الداخليتان غير المتجاورتين والواقعتين على جهتين مختلفتين من القاطع لمستقيمين متوازيين.
- الزاويتان المتناظرتان هما زاويتان إحداهما داخلية والأخرى خارجية وتقعان على جهة واحدة من القاطع لمستقيمين متوازيين.
- الزاويتان اللتان مجموع قياسيهما ٩٠ ْ هما زاويتان متتامتان.
- لزاويتان اللتان مجموع قياسيهما ١٨٠ ْ هما زاويتان متكاملتان.
مشاركة الحل
حل أسئلة مراجعة الفصل
المفردات
- الزاوية الداخلية - الزاوية الخارجية - الزاويتان المتجاورتان.
- الزاويتان المتقابلتان بالرأس - الزاويتان المتناظرتان - الزاويتان المتبادلتان.
- الزاويتان المتتامتان - الزاويتان المتكاملتان - تنصيف الزاوية.
- الدائرة - مركز الدائرة - وتر الدائرة - قطر الدائرة - نصف قطر الدائرة.
أكمل الجمل أدناه مستعملاً المفردات أعلاه:
- الزاويتان المتجاورتان هما زاويتان بينهما ضلعٌ مشتركٌ وضلعاهما الآخران في جهتين مختلفتين من الضلع المشترك.
- الدائرة هي مجموعةٌ من النقاط المتصلة في المستوى التي لها البعد نفسه عن نقطةٍ ثابتةٍ تسمى مركز الدائرة.
- القطعة المستقيمة التي طرفاها على الدائرة تسمى وتر الدائرة.
- الوتر الذي يمر بمركز الدائرة يسمى قطر الدائرة.
- القطعة المستقيمة التي تصل بين مركز الدائرة ونقطة على الدائرة تسمى نصف قطر الدائرة.
- الزاويتان المتقابلتان هما زاويتان مشتركتان في الرأس وغير متجاورتين.
- الزاويتان المتبادلتان هما الزاويتان الداخليتان غير المتجاورتين والواقعتين على جهتين مختلفتين من القاطع لمستقيمين متوازيين.
- الزاويتان المتناظرتان هما زاويتان إحداهما داخلية والأخرى خارجية وتقعان على جهة واحدة من القاطع لمستقيمين متوازيين.
- الزاويتان اللتان مجموع قياسيهما ٩٠ ْ هما زاويتان متتامتان.
- لزاويتان اللتان مجموع قياسيهما ١٨٠ ْ هما زاويتان متكاملتان.
.JPG) أحدد العلاقة بين أزواج الزوايا من الشكل المجاور.
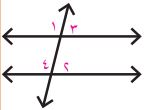
أحدد العلاقة بين أزواج الزوايا من الشكل المجاور.
- الزاوية (١، ٣) متجاورتان.
- الزاوية (٢، ٣) متناظرتان.
- الزاوية (٢، ٤) متجاورتان.
- الزاوية (١، ٤) متناظرتان.
.JPG) أحدد ما إذا كانت الزاويتين اللتان قياسيهما ٣٧ ْ، ٥٣ ْ متتامتين أو متكاملتين.
أحدد ما إذا كانت الزاويتين اللتان قياسيهما ٣٧ ْ، ٥٣ ْ متتامتين أو متكاملتين.
٣٧ + ٥٣ = ٩٠ إذاً بما أن المجموع يساوي (٩٠) فالزاويتان متتامتان.
.JPG) أستعمل المنقلة لأرسم زاوية قياسها ١٣٠ ْ ثم أنصفها.
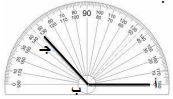
أستعمل المنقلة لأرسم زاوية قياسها ١٣٠ ْ ثم أنصفها.
- الخطوة (١): أرسم شعاعاً وأسميه (ب أ) أ ــــــــــــ ب.
- الخطوة (٢): أضع مركز المنقلة عند النقطة (ب) بحيث تقع الحافة صفر المنقلة على الشعاع (ب أ).
- الخطوة (٣): إقرأ التدريج حتى (١٣٠) وأعين نقطة على الورقة تقابل التدرج (١٣٠) ولتكن جـ.
- الخطوة (٤): أرفع المنقلة واصل باستعمال المسطرة بين النقطة جـ ورأس الزاوية ب.
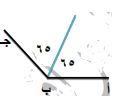
- الخطوة (٥): أقسم قياس الزاوية (١٣٠) على (٢) لأجد قياس نصف الزاوية: ١٣٠ ÷ ٢ = ٦٥.
- الخطوة (٦): أحدد باستعمال المنقلة قياس زاوية (٦٥) وأحدد نقطة على الورقة تقابل زاوية (٦٥).
- الخطوة (٧): ارسم شعاعاً من رأس الزاوية إلى النقطة (م) حددتها لأحصل على منصف الزاوية.
.JPG) أرسم المثلث أ ب جـ الذي أطوال أضلاعه هي:
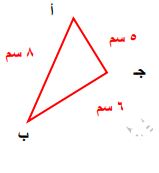
أرسم المثلث أ ب جـ الذي أطوال أضلاعه هي:
أ ب = ٨ سم، ب جـ = ٦ سم، أ جـ = ٥ سم
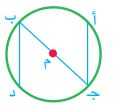
.JPG) أحدد عناصر الدائرة الموجودة في الشكل المجاور.
أحدد عناصر الدائرة الموجودة في الشكل المجاور.
- م: المركز.
- : أوتار.
- أنصاف أقطار.
- قطر.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)