حلول الأسئلة
السؤال
أستعمل الفرجار لأنصف الزاوية المعطى قياسها في كل مما يأتي:
الحل
١٥٥ ْ
- الخطوة (١): أضع رأس الفرجار عند رأس الزاوية في نقطة (ب) وافتحه بمقدار مناسب وارسم قوساً بقطع ضلعي الزاوية في النقطتين (هـ، د).
- الخطوة (٢): أضع رأس الفرجار عند النقطة (هـ) وارسم قوساً بين الضلعين بفتحة فرجار مناسبة وأكرر العملية مع تقاطع بنفس فتحة الفرجار السابقة وأسمي نقطة تقاطع القوسين (س).
- الخطوة (٣): ارسم شعاعاً بين النقطة (س) ورأس الزاوية فيكون الشعاع (ب) (س) هو نصف الزاوية (أ ب جـ).
- الخطوة (٤): أقيس الزاوية (أ ب جـ) والزاوية (جـ ب س) باستعمال المنقلة.
ألاحظ أن قياس كل من الزاويتين هو (٧٧,٥).
مشاركة الحل
حل أسئلة اختبار الفصل
أحدد العلاقة بين الزاويتين في كل شكل من الأشكال الآتية:
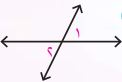
١)
متقابلتان.
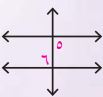
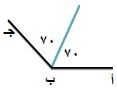
٢)
متجاورتان.
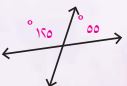
٣)
متبادلتان.
أحدد ما إذا كانت الزاويتان متتامتين أو متكاملين في كل مما يأتي:
٤)
متكاملتان.
٥٥ + ١٢٥ = ١٨٠
٥)
متتامتان.
٥٠ + ٤٠ = ٩٠
٦) إذا كانت الزاويتان ع، ل زاويتين متتامتين وكان قياس الزاوية ل = ٢٣ ْ فما قياس الزاوية ع؟
الزاويتان المتتامتان مجموع قياسهما (٩٠)
- ع + ل = ٩٠
- ع + ٢٣ = ٩٠
- ٩٠ - ٢٣ = ٦٧ قياس زاوية ع.
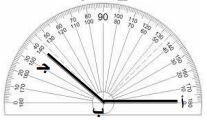
٧) أستعمل المنقلة لأرسم زاوية قياسها ١٤٠ ْ ثم أنصفها.
- الخطوة (١): أرسم شعاعاً وأسميه (ب أ) أ ــــــــــــ ب.
- الخطوة (٢): أضع مركز المنقلة عند النقطة (ب) بحيث تقع الحافة صفر المنقلة على الشعاع (ب أ).
- الخطوة (٣): أقرأ التدريج حتى (١٤٠) وأعين نقطة على الورقة تقابل التدرج (١٤٠) ولتكن جـ.
- الخطوة (٤): أرفع المنقلة واصل باستعمال المسطرة بين النقطة جـ ورأس الزاوية ب.
- الخطوة (٥): أقسم قياس الزاوية (١٤٠) على (٢) لأجد قياس نصف الزاوية: ١٤٠ ÷ ٢ = ٧٠.
- الخطوة (٦): أحدد باستعمال المنقلة قياس زاوية (٧٠) وأحدد نقطة على الورقة تقابل زاوية (٧٠).
- الخطوة (٧): ارسم شعاعاً من رأس الزاوية إلى النقطة (م) حددتها لأحصل على منصف الزاوية.
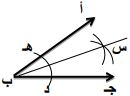
أستعمل الفرجار لأنصف الزاوية المعطى قياسها في كل مما يأتي:
٨) ٣٦ ْ
- الخطوة (١): أضع رأس الفرجار عند رأس الزاوية في نقطة (ب) وافتحه بمقدار مناسب وارسم قوساً بقطع ضلعي الزاوية في النقطتين (هـ، د).
- الخطوة (٢): أضع رأس الفرجار عند النقطة (هـ) وارسم قوساً بين الضلعين بفتحة فرجار مناسبة وأكرر العملية مع تقاطع بنفس فتحة الفرجار السابقة وأسمي نقطة تقاطع القوسين (س).
- الخطوة (٣): ارسم شعاعاً بين النقطة (س) ورأس الزاوية فيكون الشعاع (ب) (س) هو نصف الزاوية (أ ب جـ).
- الخطوة (٤): أقيس الزاوية (أ ب جـ) والزاوية (جـ ب س) باستعمال المنقلة.
ألاحظ أن قياس كل من الزاويتين هو (١٨).
٩) ٥٥ ْ
- الخطوة (١): أضع رأس الفرجار عند رأس الزاوية في نقطة (ب) وافتحه بمقدار مناسب وارسم قوساً بقطع ضلعي الزاوية في النقطتين (هـ، د).
- الخطوة (٢): أضع رأس الفرجار عند النقطة (هـ) وارسم قوساً بين الضلعين بفتحة فرجار مناسبة وأكرر العملية مع تقاطع بنفس فتحة الفرجار السابقة وأسمي نقطة تقاطع القوسين (س).
- الخطوة (٣): ارسم شعاعاً بين النقطة (س) ورأس الزاوية فيكون الشعاع (ب) (س) هو نصف الزاوية (أ ب جـ).
- الخطوة (٤): أقيس الزاوية (أ ب جـ) والزاوية (جـ ب س) باستعمال المنقلة.
ألاحظ أن قياس كل من الزاويتين هو (٢٧,٥).
١٠) ١٥٥ ْ
- الخطوة (١): أضع رأس الفرجار عند رأس الزاوية في نقطة (ب) وافتحه بمقدار مناسب وارسم قوساً بقطع ضلعي الزاوية في النقطتين (هـ، د).
- الخطوة (٢): أضع رأس الفرجار عند النقطة (هـ) وارسم قوساً بين الضلعين بفتحة فرجار مناسبة وأكرر العملية مع تقاطع بنفس فتحة الفرجار السابقة وأسمي نقطة تقاطع القوسين (س).
- الخطوة (٣): ارسم شعاعاً بين النقطة (س) ورأس الزاوية فيكون الشعاع (ب) (س) هو نصف الزاوية (أ ب جـ).
- الخطوة (٤): أقيس الزاوية (أ ب جـ) والزاوية (جـ ب س) باستعمال المنقلة.
ألاحظ أن قياس كل من الزاويتين هو (٧٧,٥).
أي من الأطوال الآتية يمكن أن تكون أطوال أضلاع مثلث؟
١١) ٦ سم، ٧ سم، ٤ سم.
أتحقق من أن مجموع طولي ضلعين أكبر من طول الضلع الثالث:
- ٦ + ٧ = ١٣ أكبر من طول الضلع الثالث ٤ سم.
- ٦ + ٤ = ١٠ أكبر من طول الضلع الثالث ٧ سم.
- ٧ + ٤ = ١١ أكبر من طول الضلع الثالث ٦ سم.
لذا يمكن رسم مثلث باستعمال هذه الأطوال.
١٢) ٨ سم، ١٦ سم، ٥ سم.
أتحقق من أن مجموع طولي ضلعين أكبر من طول الضلع الثالث:
- ٨ + ١٦ = ٢٤ أكبر من طول الضلع الثالث ٥ سم.
- ٨ + ٥ = ١٣ أصغر من طول الضلع الثالث ١٦ سم.
لذا يمكن رسم مثلث باستعمال هذه الأطوال.
١٣) ١٥ سم، ٤ سم، ١٠ سم.
أتحقق من أن مجموع طولي ضلعين أكبر من طول الضلع الثالث:
- ١٥ + ٤ = ١٩ أكبر من طول الضلع الثالث ١٠ سم.
- ١٥ + ١٠ = ٢٥ أكبر من طول الضلع الثالث ٤ سم.
- ٤ + ١٠ = ١٤ أصغر من طول الضلع الثالث ١٥ سم.
لذا يمكن رسم مثلث باستعمال هذه الأطوال.
١٤) ٩ سم، ٦ سم، ٤ سم.
أتحقق من أن مجموع طولي ضلعين أكبر من طول الضلع الثالث:
- ٩ + ٦ = ١٥ أكبر من طول الضلع الثالث ٤ سم.
- ٩ + ٤ = ١٣ أكبر من طول الضلع الثالث ٦ سم.
- ٦ + ٤ = ١٠ أكبر من طول الضلع الثالث ٩ سم.
لذا يمكن رسم مثلث باستعمال هذه الأطوال.
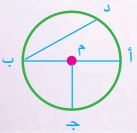
١٥) أحدد عناصر الدائرة الموجودة في الشكل المجاور:
- م: المركز.
- : قطر الدائرة.
- : وتر في الدائرة.
- : نصف قطر في الدائرة.

.JPG)