الدوال الحقيقية
مفهوم الدالة: Concept of the function:
تسمى العلاقة من مجموعة (A) إلى مجموعة (B) إنها دالة إذا كان لكل عنصر من عناصر (A) له صورة وحيدة في المجموعة (B) أي يظهر مرة واحدة في كل زوج من بيان العلاقة:
ونعبر عن الدالة رياضياً من المجموعة A إلى المجموعة B بالدالة f حيث: وتقرأ (f دالة من A إلى B)
، يوجد وحيد أو
ملاحظات:
- إذا كان الزوج المرتب x,y) ordered pair) ينتمي إلى بيان الدالة f. فإن هو صورة Image العنصر x تحت تأثير الدالة f
- تتعين الدالة f إذا توفرت ثلاث مكونات هي:
أ- المجال Domain وهو المجموعة A التي ينتمي إليها العنصر x حيث (x,y) ينتمي إلى بيان الدالة.
ب- المجال المقابل Codomain وهو المجموعة B التي ينتمي إليها العنصر y.
ج- قاعدة الدالة f والتي تسمى قاعدة الاقتران التي تربط عناصر المجموعة A بعناصر المجموعة B
- قاعدة الدالة تعطى بإحدى الطريقتين:
أ- ذكر بيان الدالة وتكتب على شكل أزواج مرتبة.
ب- ذكر معادلة تربط المتغير (x) بالمتغير (y).
الدوال الحقيقية: Real function:
تسمى الدالة f حقيقية إذا كان كل من مجالها (A) ومجالها المقابل ( B ) مجموعة جزئية غير خالية من مجموعة الأعداد الحقيقية R
- المجال =
- المجال المقابل مجموعة جزئية من R
أوسع مجال الدالة:
هي جميع العناصر من المجال التي تحقق الدالة وفي هذه الحالة:
1- جد مجال الدالة
أو مجال R
=f جميع الأعداد الحقيقية أي إذا كانت الدالة f خالية من الكسور فإن:
أوسع مجال للدالة R=f
2- جد مجال الدالة
مجال الدالة
تكون الدالة معرفة في R إذا كان
أوسع مجال للدالة
أي إذا كانت الدالة f جذرية فإن أوسع مجال يكون ما تحت الجذر
3- جد مجال f إذا كان
مجال
معرفة دائماً في R مهما كان
مجال R=f (الدالة خالية من الكسور والجذور)
4- جد مجال الدالة
مجال
ولكن معرفة في R ماعدا 1=x
مجال R\{1}=f
إذا كانت الدالة كسرية فإن أوسع مجال هو R ما عدا القيم التي تجعل المقام = صفراً.
التمثيل البياني للدالة:
إذا كانت فإن منحني الدالة f(x)=y هو مجموعة النقط (x,y) في المستوى الديكارتي.
5- ارسم منحني الدالة حيث
نعين عدد من الأزواج المرتبة ((x,f(x)) ممكن أن يكون الجدول أفقياً
| y | x |
| (6- | 0) |
| (3- | 1) |
| (0 | 1) |
| (9- | 1-) |
| (12- | 2-) |
6- مثل الدالة بحيث بيانياً
بما أن الدالة خطية فهي تمثل مستقيم لذلك نختار نقطتين (1-,1)،(3-,2)
| y | x |
| (1- | 1) |
| (3- | 2) |
7- مثل الدالة بحيث بيانياً
في الدالة التربيعية نعين خمس نقاط على الأقل:
|
... |
3 |
2 |
1 |
0 |
1- |
2- |
3- |
... |
x |
|
... |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
... |
y |
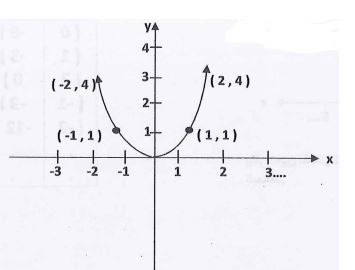
نعين النقط (x,y) على المستوي ونصل بينها بمنحني فهو يمثل الدالة f بيانياً.
المنحني متناظر حول محور الصادات والتمثيل البياني لمنحني الدالة f=x2 يسمى قطعاً مكافئاً (parabola)
8- مثل الدالة بحيث بيانياً
نعين نقاط المنحني وهو يمثل المنحني منسحباً 3 وحدات في الاتجاه الموجب لمحور الصادات
|
... |
3 |
2 |
1 |
0 |
1- |
2- |
3- |
... |
x |
|
... |
12 |
7 |
4 |
3 |
4 |
7 |
12 |
... |
y |
نحدد النقاط على المستوي
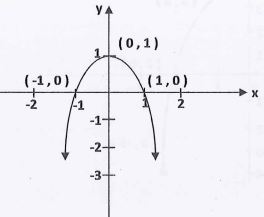
9- مثل الدالة بحيث بيانياً
إن مجال الدالة هو R وعلى ذلك فإن التمثيل البياني يمكن أن ينتج عن المنحني قطع مكافئ رأسه في نقطة الأصل ومحدب وبانسحاب إلى الأعلى واحد وحدة طول.
| y | x |
| (3- | 2-) |
| (0 | 1-) |
| (1 | 0) |
| (0 | 1) |
| (3- | 2) |

.JPG)

.JPG)
.JPG)