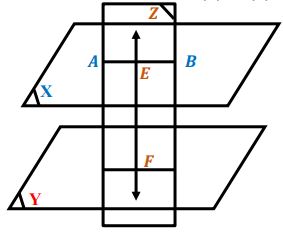
برهن أن المستوي العمودي على أحد مستويين متوازيين يكون عمودياً على الآخر أيضاً.

المعطيات: $\left(Z\right)\cap \left(\mathrm{X}\right)=\overleftrightarrow{AB},\left(Z\right)\perp \left(\mathrm{X}\right),\text{(X)}//\left(\mathrm{Y}\right)$

المطلوب إثباته: $\text{(Z)}\perp \left(\mathrm{Y}\right)$

البرهان: نرسم $\overleftrightarrow{EF}\subset \left(\mathrm{Z}\right)$ بحيث $\overleftrightarrow{EF}\perp \overleftrightarrow{AB}$ (في المستوي الواحد يمكن رسم مستقيم وحيد عمودي على مستقيم معلوم من نقطة معلومة).

• $\left(Z\right)\perp \left(\mathrm{X}\right)\because$ (معطى).
• $\overleftrightarrow{EF}\perp \left(\mathrm{X}\right)$ (إذا تعامد مستويان فالمستقيم المرسوم ل أحدهما والعمودي على مستقيم التقاطع يكون عمودي على الآخر).
• $\left(\mathrm{X}\right)//\left(\mathrm{Y}\right)\because$ (معطی).
• $\overleftrightarrow{EF}\perp \left(\mathrm{Y}\right)\therefore$ (المستقيم العمودي على أحد مستويين متوازيين يكون عمودياً على الآخر أيضاً).
• $\left(\mathrm{Z}\right)\perp \left(\mathrm{X}\right)\therefore$ (يتعامد المستويان إذا احتوى أحدهما على مستقيم وكان عمودياً على الآخر) (و- هـ. م).

تمارين (1-6)

تمارين (1-6)

(1)- برهن أن مستوي الزاوية المستوية العائدة لزاوية زوجية يكون عمودياً على حرفها.

المعطيات:

• الزاوية الزوجية $\left(\mathrm{X}\right)-\overleftrightarrow{\mathrm{AB}}-\left(\mathrm{Y}\right)$
• والزاوية المستوية العائدة لها $<)CDE$

المطلوب إثباته: $\overline{AB}\perp \left(\mathrm{Z}\right)$

البرهان: $<)CDE$ زاوية عائدة للزاوية الزوجية $\left(\mathrm{X}\right)-\overleftrightarrow{\mathrm{AB}}-\left(\mathrm{Y}\right)$ (معطى)

$\begin{array}{rl}& \overline{AB}\perp \overline{DC}\\ & \overline{AB}\perp \overline{DE}\end{array}$

(من تعريف الزاوية العائدة لزاوية زوجية).

(هي الزاوية الناتجة من اتحاد شعاعين عموديين على حرف الزاوية الزوجية من نقطة تنتمي إليه وكل منهما في أحد وجهي الزاوية الزوجية).

ليكن $\left(Z\right)$ مستوي المستقيمين المتقاطعين $CD,DE$ (لكل مستقيمين متقاطعين يوجد مستو وحيد يحتويهما).

$\overline{AB}\perp \left(Z\right)\therefore$ (المستقيم العمودي على مستقيمين متقاطعين من نقطة تقاطعهما يكون عمودياً على مستويهما).

(و. هـ. م)

(2)- برهن أنه إذا وازی مستقيم مستوياً وكان عمودياً على مستو آخر فإن المستويين متعامدان.

المعطيات: $\overline{AB}//\left(\mathrm{Y}\right),\overline{AB}\perp \left(\mathrm{X}\right)$

المطلوب إثباته: $\left(\mathrm{X}\right)\perp \left(\mathrm{Y}\right)$

البرهان: لتكن $\mathrm{C}\subset \left(\mathrm{Y}\right)$ نرسم $\overleftrightarrow{CD}\perp \left(\mathrm{X}\right)$ (يمكن رسم مستقيم وحيد..).

• $\overleftrightarrow{AB}\perp \left(\mathrm{X}\right)\because$ (معطی).
• $AB//CD$ (المستقيمان العموديان على مستوي واحد متوازيان).
• $C\subset \left(Y\right)\Rightarrow \overleftrightarrow{CD}\subset \left(\mathrm{Y}\right)\therefore$ (إذا وازی مستقيم مستوياً معلوماً فالمستقيم المرسوم من أية نقطة من نقط المستوي الموازي للمستقيم المعلوم يكون محتوى فيه).
• $\left(\mathrm{X}\right)\perp \left(\mathrm{Y}\right)\therefore$ (يتعامد المستويان احتوى أحدهما على مستقيم وكان عمودياً على الآخر) (و. هـ. م).

(3)- برهن أن المستوي العمودي على أحد مستويين متوازيين يكون عمودياً على الآخر أيضاً.

المعطيات: $\left(Z\right)\cap \left(\mathrm{X}\right)=\overleftrightarrow{AB},\left(Z\right)\perp \left(\mathrm{X}\right),\text{(X)}//\left(\mathrm{Y}\right)$

المطلوب إثباته: $\text{(Z)}\perp \left(\mathrm{Y}\right)$

البرهان: نرسم $\overleftrightarrow{EF}\subset \left(\mathrm{Z}\right)$ بحيث $\overleftrightarrow{EF}\perp \overleftrightarrow{AB}$ (في المستوي الواحد يمكن رسم مستقيم وحيد عمودي على مستقيم معلوم من نقطة معلومة).

• $\left(Z\right)\perp \left(\mathrm{X}\right)\because$ (معطى).
• $\overleftrightarrow{EF}\perp \left(\mathrm{X}\right)$ (إذا تعامد مستويان فالمستقيم المرسوم ل أحدهما والعمودي على مستقيم التقاطع يكون عمودي على الآخر).
• $\left(\mathrm{X}\right)//\left(\mathrm{Y}\right)\because$ (معطی).
• $\overleftrightarrow{EF}\perp \left(\mathrm{Y}\right)\therefore$ (المستقيم العمودي على أحد مستويين متوازيين يكون عمودياً على الآخر أيضاً).
• $\left(\mathrm{Z}\right)\perp \left(\mathrm{X}\right)\therefore$ (يتعامد المستويان إذا احتوى أحدهما على مستقيم وكان عمودياً على الآخر) (و- هـ. م).

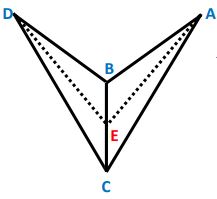
(4)- $A,B,C,D$ أربع نقاط ليست في مستو واحد بحيث $E\in \overline{BC},AB=AC$ فإذا كانت $<)AED$ عائدة للزاوية الزوجية $A-\overline{BC}-D$ برهن $CD=BD$.

المعطيات:

• $A,B,C,D$ أربع نقاط مختلفة ليست في مستو واحد.
• $<)AED,E\in \overline{BC},AB=AC$ عائدة للزاوية الزوجية $A-\overline{BC}-D$

المطلوب إثباته: $CD=BD$

البرهان:

• $AB=AC$ (معطی).
• $\overleftrightarrow{AE}\perp \overleftrightarrow{BC}$ (حسب تعريف الزاوية العائدة).
• $\overleftrightarrow{\mathrm{BE}}=\overleftrightarrow{CE}$ (العمود النازل من رأس المثلث المتساوي الساقين على القاعدة ينصفها).
• $\overleftrightarrow{DE}\perp \overleftrightarrow{BC}$ (حسب تعريف الزاوية العائدة).

المثلثان $DEC,DEB$ فيهما: $m\sphericalangle DEC=m\sphericalangle DEB$ (قوائم).

$\text{ED}$ ضلع مشترك في المثلثين.

المثلثان $DEC,DEB$ متطابقان (يتطابق المثلثان بضلعين وزاوية محصورة بينهما).

ومن التطابق ينتج $\mathrm{CD}=\mathrm{BD}$ (و . هـ. م)

(5)- برهن أنه إذا وازى كل من مستقيمين متقاطعين مستوياً معلوماً وكانا عمودين على مستويين متقاطعين فإن مستقيم المستويين المتقاطعين يكون عمودياً على المستوي المعلوم.

المعطيات:

$$\begin{gathered} AB//\left(Z\right),AC//\left(Z\right) \\ \left(\mathrm{X}\right)\cap \left(\mathrm{Y}\right)=\overline{EF},\overline{AB}\perp \left(\mathrm{X}\right),\overline{AC}\perp \left(\mathrm{Y}\right) \end{gathered}$$

المطلوب إثباته: $\overleftrightarrow{EF}\perp \left(Z\right)$

البرهان:

• $\overline{AB},\overline{AC}=\mathrm{M}$ (لكل مستقيمين متقاطعين يحتويهما مستو وحيد يحتويهما).
• $AB,AC//\left(Z\right)\because$ (معطی).
• $\left(Z\right)//\left(M\right)\therefore$ (إذا كان كل من مستقيمين متقاطعين يوازيان مستوياً معلوماً فإن مستويهما يوازي المستوى المعلوم).
• $\overline{AB}\perp \left(\mathrm{X}\right)$ (معطی)، $\overline{AB}\subset \mathrm{M}$ (بالبرهان).
• $\left(\mathrm{M}\right)\perp \left(\mathrm{X}\right)$ (يتعامد المستويان إذا احتوى أحدهما على مستقيم وكان عمودياً على الآخر).
• $\overline{AC}\perp \left(Y\right)$ (معطی) $\overline{AC}\subset M$ (بالبرهان).
• $\left(\mathrm{M}\right)\perp \left(\mathrm{Y}\right)$ (يتعامد المستويان إذا احتوى أحدهما على مستقيم وكان عمودياً على الآخر).
• $\overleftrightarrow{EF}\perp \left(\mathrm{M}\right)$ (إذا كان كل من مستويين متقاطعين عمودياً على مستو ثالث فإن مستقيم تقاطعهما يكون عمودياً على المستوي الثالث).
• $\overleftrightarrow{EF}\perp \left(\mathrm{Z}\right)$ (المستقيم العمودي على أحد مستويين متوازيين يكون عمودياً على المستوى الآخر) (و، هـ، م).

(6)- دائرة قطرها $\overline{AC},\overline{AB}$ عمودي على مستويها، $\text{D}$ نقطة تنتمي للدائرة برهن أن $\left(CDA\right)\perp \left(CDB\right)$.

المعطيات:

• $\overline{AB}$ قطرة في دائرة، (مستوي الدائرة) $\overline{AC}\perp$
• $D$ نقطة تنتمي للدائرة

المطلوب إثباته: $\left(CDA\right)\perp \left(CDB\right)$

البرهان:

• $<)ADB\because$ زاوية محيطية مرسومة في نصف دائرة قياسها ${90}^{\circ }$
• (لأن قياس الزاوية المحيطية يساوي نصف قياس الزاوية المركزية).
• $\overline{AD}\perp \overline{DB}$ (إذا كانت الزاوية بين مستقيمين قائمة فإن المستقيمين متعامدين).
• $\overline{AC}$ عمودي على مستوى الدائرة (معطى).
• $\overline{CD}\perp \overline{DB}$ (مبرهنة الأعمدة الثلاثة).
• أصبح لدينا كلاً من $\overline{CD},\overline{AD}\perp \overline{DB}$ (بالبرهان).
• $\overline{DB}\perp CDA$ (المستقيم العمودي على مستقيمين متقاطعين من نقطة تقاطعهما يكون عمودياً على مستويهما).
• لكن $\overline{DB}\subset \left(CDB\right)$
• $\left(CDA\right)\perp \left(CDB\right)$ (كل مستوي مار بمستقيم عمودي على مستوي معلوم يكون عمودياً عليه) (و . هـ . م).