حلول الأسئلة
السؤال
جد قياس الزاوية الزوجية
الحل
المعطيات:
المطلوب إثباته: إيجاد قياس الزاوية الزوجية
البرهان: في المستوي نرسم في نقطة (المستوي الواحد يوجد مستقيم وحيد عمودي على آخر من نقطة معلومة).
- (معطی).
- (مبرهنة الأعمدة الثلاثة).
عائدة للزاوية الزوجية (تعريف الزاوية العائدة).
(المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المحتواة في المستوي والمارة من أثره).
القائم الزاوية في
القائم الزاوية في
قائم الزاوية في :
قياس
قياس الزاوية الزوجية
(قياس الزاوية الزوجية هو قياس الزاوية العائدة لها وبالعكس).
(و . هـ . م)
مشاركة الحل
الزاوية الزوجية والمستويات العامودية
الزاوية الزوجية والمستويات العامودية
الزاوية الزوجية: اتحاد نصفي مستويين لهما حافة مشتركة.
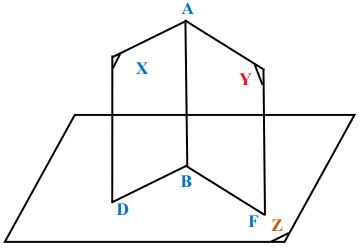
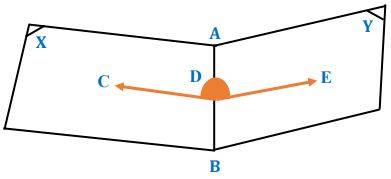
وتسمى الحافة المشتركة بـ (حرف الزاوية الزوجية) ويسمى كل من نصفي المستويين بـ (وجه الزاوية الزوجية) كما في الشكل:
حيث هو حرف الزاوية الزوجية.
هما وجهاها، ويعبر عن الزاوية الزوجية بالتعبير: وقد يعبر عنها بحرف الزاوية الزوجية إن لم يكن مشتركاً مع زاوية أخرى فمثلاً:
الزاوية الزوجية:
ولا يمكن أن تكتب الزاوية الزوجية بشكل في هذا المثال لأن الحرف مشترك في أكثر من زاوية زوجية.
ملاحظة: عندما تكون أربع نقاط ليست في مستو واحد، تكتب الزاوية الزوجية أو الزاوية الزوجية بين المستويين أو كما في الشكل.
وتقاس الزاوية الزوجية كالآتي: نأخذ نقطة على الحافة المشتركة ونرسم من العمود في والعمود في على الحرف فيكون قياس الزاوية الزوجية بين المستويين هو قياس الزاوية وتسمى الزاوية الزاوية العائدة للزاوية الزوجية، كما في الشكل:
بعبارة أخرى لدينا الزاوية الزوجية
ولدينا:
هي الزاوية العائدة للزاوية الزوجية أو .
الزاوية المستوية العائدة لزاوية زوجية: هي الزاوية التي ضلعاها عموديان على حرف الزاوية الزوجية من نقطة تنتمي إليه وكل منهما في أحد وجهي الزاوية الزوجية.
أو هي اتحاد شعاعين عموديين على حرف الزاوية الزوجية من نقطة تنتمي إليه وكل منهما في أحد وجهي الزاوية الزوجية.
ومن تعريف الزاويتين العائدة والزوجية يمكن استنتاج الآتي:
- قياس زاوية عائدة لزاوية زوجية ثابت.
- قياس الزاوية الزوجية يساوي قياس الزاوية العائدة لها وبالعكس.
ملاحظة:
- إذا كانت الزاوية الزوجية قائمة فإن المستويين متعامدان وبالعكس. (نستفاد منها في إثبات مبرهنة 7) قياس وكذلك قياس الزاوية العائدة .
- كل مستويان متعامدان يجب أن يكونا متقاطعان لكن العكس ليس بالضرورة.
مبرهنة (7): إذا تعامد مستويان فالمستقيم المرسوم لا أحدهما والعمودي على مستقيم التقاطع يكون عمودياً على المستوى الآخر.
المعطيات: في نقطة
المطلوب إثباته:
البرهان:
في نرسم (في المستوي الواحد يمكن رسم مستقيم وحيد عمودي على مستقيم فيه من نقطة معلومة).
(معطی)
عائدة للزاوية الزوجية (تعريف الزاوية العائدة).
- (قياس الزاوية الزوجية يساوي قياس الزاوية العائدة لها وبالعكس).
- (إذا كان قياس الزاوية بين مستقيمين فإن المستقيمين متعامدان وبالعكس).
- (المستقيم العمودي على مستقيمين متقاطعين من نقطة تقاطعهما يكون عمودياً على مستويهما).
(و . هـ . م)
نتيجة مبرهنة 7: إذا تعامد مستويان فالمستقيم المرسوم من نقطة في أحدهما عمودياً على المستوي الآخر يكون محتوى فيه.
المعطيات:
المطلوب إثباته:
البرهان:
إذا لم يكن نرسم وعمودي على
(في المستوي الواحد يمكن رسم مستقيم وحيد عمودي على مستقيم معلوم من نقطة معلومة).
- (معطی)
- (مبرهنة 7) (إذا تعامد مستويان فالمستقيم المرسوم في أحدهما والعمودي على مستقيم التقاطع يكون عمودياً على المستوى الآخر)
- (معطى)
- (في المستوى الواحد يمكن رسم مستقيم وحيد عمودي على مستو معلوم من نقطة لا تنتمي إليه)
- (و . هـ . م)
مبرهنة (8):
- كل مستو مار بمستقيم عمودي على مستو آخر يكون عمودياً على ذلك المستوي.
- (يتعامد المستويان إذا احتوى أحدهما على مستقيم عمودي على الآخر).
المعطيات:
المطلوب إثباته:
البرهان:
- ليكن (يتقاطع المستويان بخط مستقيم).
- (مستقيم التقاطع يحتوي على النقاط المشتركة).
في نرسم (في المستوي الواحد يوجد مستقيم وحيد عمودي على مستقيم فيه من نقطة معلومة).
- (معطی)
- المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المحتواة لا المستوي والمارة من أثره).
- (معطی).
- عائدة للزاوية الزوجية (تعريف الزاوية العائدة).
- (لأن )
قياس الزاوية الزوجية (قياس الزاوية الزوجية يساوي قياس الزاوية العائدة لها وبالعكس).
(إذا كان قياس الزاوية الزوجية فإن المستويين متعامدان وبالعكس) (و . هـ . م)
مبرهنة (9): من مستقيم غير عمودي على مستو معلوم يوجد مستو وحيد عمودي على المستوى المعلوم.
المعطيات: غير عمودي على
المطلوب إثباته: إيجاد مستو وحيد يحوي وعمودي على
البرهان:
من نقطة نرسم
(يوجد مستقيم وحيد عمودي على مستو معلوم من نقطة لا تنتمي إليه).
متقاطعان فيوجد مستو وحيد مثل يحتويهما (لكل مستقيمين متقاطعين يوجد مستو وحيد يحتويهما).
(بالبرهان)
(مبرهنة 8) (يتعامد المستويان إذا احتوى أحدهما على مستقيم عمودي على الآخر).
ولبرهنة الوحدانية: نفرض وجود مستوى آخر يحوي وعمودي على
- (بالبرهان)
- (نتيجة مبرهنة 7)
(لكل مستقيمين متقاطعين يوجد مستو وحيد يحويهما) و . هـ . م)
نتيجة مبرهنة (9): إذا كان كل من مستويين متقاطعين عمودياً على مستو ثالث فإن مستقيم تقاطعهما يكون عمودياً على المستوى الثالث.
المعطيات:
المطلوب إثباته:
البرهان: إذا لم يكن
لما وجد أكثر مستوي يحوي وعمودي على (مبرهنة 9).
(من مستقيم غير عمودي على مستو معلوم يمكن رسم مستو وحيد عمودي على المستوي المعلوم).
(و . هـ . م)
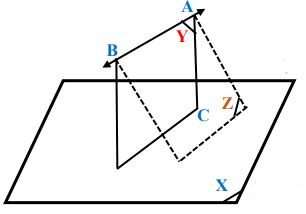
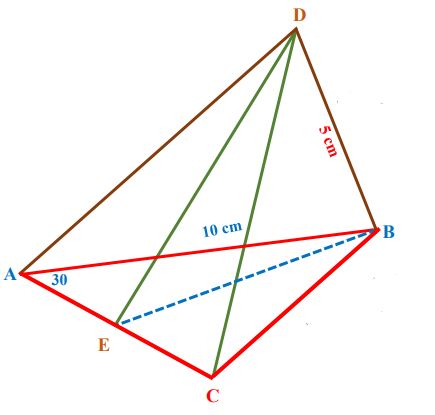
(1)- في
جد قياس الزاوية الزوجية
المعطيات:
المطلوب إثباته: إيجاد قياس الزاوية الزوجية
البرهان: في المستوي نرسم في نقطة (المستوي الواحد يوجد مستقيم وحيد عمودي على آخر من نقطة معلومة).
- (معطی).
- (مبرهنة الأعمدة الثلاثة).
عائدة للزاوية الزوجية (تعريف الزاوية العائدة).
(المستقيم العمودي على مستوي يكون عمودياً على جميع المستقيمات المحتواة في المستوي والمارة من أثره).
القائم الزاوية في
القائم الزاوية في
قائم الزاوية في :
قياس
قياس الزاوية الزوجية
(قياس الزاوية الزوجية هو قياس الزاوية العائدة لها وبالعكس).
(و . هـ . م)
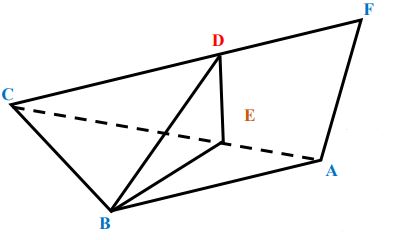
(2)- ليكن مثلثاً وليكن
برهن أن:
المعطيات:
المطلوب إثباته:
البرهان:
- (معطی).
- (مبرهنة 8) (يتعامد المستويان إذا احتوى أحدهما على مستقيم عمودي على الآخر).
- (معطی).
- (مبرهنة 7) (إذا تعامد مستويان فالمستقيم المرسوم في أحدهما والعمودي على مستقيم التقاطع يكون عمودياً على الآخر).
- (معطی).
- (نتيجة مبرهنة الأعمدة الثلاثة) (و . هـ . م).
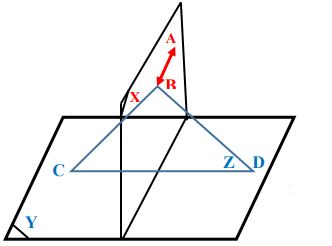
(3)- مستويان متعامدان
عموديان على ويقطعان في على الترتيب. برهن أن
المعطيات: إن عموديان على ويقطعان في على الترتيب.
المطلوب إثباته:
البرهان: ليكن مستوي المستقيمين المتقاطعين
(لكل مستقيمين متقاطعين يوجد مستوياً وحيداً يحويهما).
- (معطی).
- (المستقيم العمودي على مستقيمين متقاطعين من نقطة تقاطعهما يكون عمودياً على مستويهما).
- (معطی)
- (يتعامد المستويان إذا احتوى أحدهما على مستقيم عمودي على الآخر).
- (معطی)
ولما كان (لأنه محتوى في كل منهما).
(إذا كان كل من مستويين متقاطعين على مستو ثالث فإن مستقيم تقاطعهما يكون عمودياً على المستوي الثالث) (و . هـ . م).

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)