حلول الأسئلة
السؤال
خزان على شكل متوازي سطوح مستطيلة طول قاعدته ضعف عرضها فإذا كانت مساحة المعدن المستخدم في صناعته جد أبعاد الخزان لكي يكون حجمه أكبر ما يمكن علماً أن الخزان ذو غطاء كامل.
الحل
الفرضية:
- نفرض عرض القاعدة = x
- نفرض طول القاعدة (ضعف عرضها) = 2x
- نفرض الارتفاع = y
- نفرض حجم الخزان = V
الدالة: حجم الخزان.
العلاقة: مساحة المعدن = المساحة الجانبية + مساحة القاعدتين
المساحة الجانبية = محيط القاعدة × الارتفاع
مشاركة الحل
تمارين (6-3)
تمارين (6-3)
(1)- جد عددين موجبين مجموعهما وحاصل ضرب أحدهما في مربع الآخر أكبر ما يمكن.
الفرضية:
- نفرض العدد الأول =
- نفرض العدد الثاني =
الدالة: = حاصل ضرب العدد الأول × مربع العدد الثاني
العلاقة: مجموع العددين
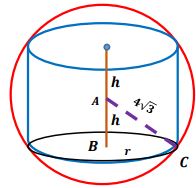
(2)- جد ارتفاع أكبر أسطوانة دائرية قائمة توضع داخل كرة نصف قطرها .
الفرضية:
- نفرض الارتفاع =
- نفرض نصف قطر الاسطوانة =
- نفرض الحجم =
الدالة: قانون حجم الأسطوانة (هي التي تقوم باشتقاقها).
حجم الأسطوانة = مساحة القاعدة × الارتفاع.
العلاقة: نظرية فيثاغورس على المثلث القائم
(3)- جد بعدي أكبر مستطيل يوضع داخل نصف دائرة قطرها .
الفرضية:
- نفرض طول المستطيل =
- نفرض عرض المستطيل =
- نفرض مساحة المستطيل =
الدالة: قانون مساحة المستطيل (هي التي تقوم باشتقاقها).
العلاقة: نظرية فيثاغورس على المثلث القائم
(4)- جد أبعاد أكبر مساحة المثلث متساوي الساقين طول كل من ساقيه = .
الفرضية:
- نفرض ارتفاع المثلث =
- نفرض طول ضلع المثلث =
- نفرض مساحة المثلث =
الدالة: قانون مساحة المثلث (هي التي نقوم باشتقاقها).
العلاقة: مبرهنة فيثاغورس.
(5)- جد أقل محيط ممكن للمستطيل الذي مساحته .
الفرضية:
- نفرض طول المستطيل =
- نفرض عرض المستطيل =
- نفرض مساحة المستطيل =
- نفرض محيط المستطيل =
الدالة: هي محيط المستطيل (هي التي تقوم باشتقاقها) محيط المستطيل = 2 × (الطول + العرض).
العلاقة: مساحة المستطيل.
(6)- جد حجم أكبر مخروط دائري قائم يمكن وضعه داخل كرة نصف قطرها .
الفرضية:
- نفرض نصف قطر المخروط =
- نفرض ارتفاع المخروط =
- نفرض حجم المخروط =
الدالة: قانون حجم المخروط.
العلاقة: مبرهنة فيثاغورس للمثلث القائم الزاوية
(7)- جد معادلة المستقيم الذي يمر من النقطة والذي يصنع مع المحوريين في الربع الأول أصغر مثلث.
الفرضية:
- نقرض النقطة نقطة تقاطع المستقيم مع المحور السيني.
- نفرض النقطة نقطة تقاطع المستقيم مع المحور الصادي.
- نفرض أبعاد المثلث =
- نفرض مساحة المثلث =
الدالة: قانون مساحة المثلث.
العلاقة: قانون الميل (ميل = میل )
النقطة تنتمي للمستقيم
نقطة تقاطع المستقيم مع المحور السيني.
نقطة تقاطع المستقيم مع المحور الصادي.
(8)- جد بعدي أكبر مستطيل يوضع داخل المنطقة المحددة ومحور السينات، رأسان من رؤوسه على المنحني والرأسان الآخران على محور السينات، ثم جد محيطه.
الفرضية:
- نفرض طول المستطيل =
- نفرض عرض المستطيل =
- نفرض مساحة المستطيل =
الدالة: قانون مساحة المستطيل
مساحة المستطيل = الطول × العرض
العلاقة: المعادلة
(9)- جد أبعاد أكبر أسطوانة دائرية قائمة توضع داخل مخروط دائري قائم ارتفاعه وطول قطر قاعدته .
الفرضية:
- نفرض ارتفاع الاسطوانة =
- نفرض نصف قطر قاعدتها =
- نفرض حجم المخروط =
الدالة: الحجم = مساحة القاعدة × الارتفاع
العلاقة: تشابه المثلثان
(10)- جد حجم أكبر مخروط دائري قائم ناتج منه دوران مثلث قائم الزاوية طول وتره دوران دورة كاملة حول أحد ضلعيه القائمين.
الفرضية:
- نفرض ارتفاع المخروط =
- نفرض نصف قطر قاعدته =
- نفرض حجم المخروط =
الدالة: قانون حجم المخروط.
العلاقة: مبرهنة فيثاغورس للمثلث القائم الزاوية.
(11)- علبة أسطوانية الشكل مفتوحة من الأعلى سعتها جد أبعادها عندما تكون مساحة المعدن المستخدم في صناعتها أقل ما يمكن.
الفرضية:
- نفرض ارتفاع الاسطوانة =
- نفرض نصف قطر الاسطوانة =
- نفرض المساحة الكلية بدون غطاء =
- نفرض حجم الاسطوانة =
الدالة: قانون المساحة المساحة الكلية = المساحة الجانبية + مساحة قاعدة واحدة.
العلاقة: قانون حجم الاسطوانة الحجم = مساحة القاعدة × الارتفاع
(12)- خزان على شكل متوازي سطوح مستطيلة طول قاعدته ضعف عرضها فإذا كانت مساحة المعدن المستخدم في صناعته جد أبعاد الخزان لكي يكون حجمه أكبر ما يمكن علماً أن الخزان ذو غطاء كامل.
الفرضية:
- نفرض عرض القاعدة = x
- نفرض طول القاعدة (ضعف عرضها) = 2x
- نفرض الارتفاع = y
- نفرض حجم الخزان = V
الدالة: حجم الخزان.
العلاقة: مساحة المعدن = المساحة الجانبية + مساحة القاعدتين
المساحة الجانبية = محيط القاعدة × الارتفاع

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)