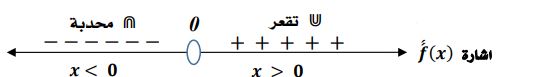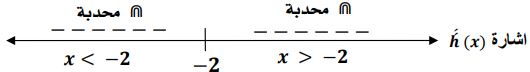جد مناطق التقعر والتحدب ونقاط الانقلاب (إن وجدت) للدوال الآتية:

$f\left(x\right)=4x^3-x^4$

$\begin{array}{rl}& f\text{'}\left(x\right)=12x^2-4x^3\\ & f^{\prime \prime }\left(x\right)=24x-12x^2\left(f^{\prime \prime }\right(x)=0 \left(\mathrm{نجعل}\right))\\ & [24x-12x^2=0]÷12\Rightarrow 2x-x^2=0\\ & x(2-x)=0\\ & either x=0\\ & \text{or }2-x=0\Rightarrow x=2\end{array}$

نقطة انقلاب $\left(0,0\right)$

$f\left(0\right)=4(0{)}^3-(0{)}^4=0$

نقطة انقلاب $\left(2,16\right)$

$f\left(2\right)=4(2{)}^3-(2{)}^4=32-16=16$

مقعرة في الفترة $(0,2)$

محدبة في $\{x:x<0\} , \{x:x>2\}$

تقعر وتحدب المنحنيات ونقط الانقلاب

تقعر وتحدب المنحنيات ونقط الانقلاب

إذا كانت $f$ دالة قابلة للاشتقاق في الفترة المفتوحة $(a,b)$ فيقال عن الدالة $f$ بأنها محدية اذا كانت $f^{\mathrm{\prime }}\left(x\right)$ متناقصة خلال تلك الفترة وتسمى مقعرة إذا كانت $f^{\mathrm{\prime }}\left(x\right)$ متزايدة خلال تلك الفترة.

ملاحظة: لإيجاد مناطق التقعر والتحدب ونقاط الانقلاب نتبع ما يلي:

1. نجد $f^{\prime \prime }\left(x\right)$ ونضعها تساوي صفراً ونستخرج قيم $x$
2. إذا كانت $f^{\prime \prime }\left(x\right)$ موجبة $\left[f^{\prime \prime }\right(x)>0]$ فالدالة مقعرة.
3. إذا كانت $f^{\prime \prime }\left(x\right)$ سالبة $\left[f^{\prime \prime }\right(x)<0]$ فالدالة محدبة.
4. نعوض قيم $x$ في الدالة الاصلية $f\left(x\right)$ لإيجاد نقطة الانقلاب.
5. إذا لم يحدث تغير في إشارة المشتقة الثانية فلا توجد هناك نقاط انقلاب للدالة.
6. إذا كانت المشتقة الثانية مجموع مربعين فإن الدالة مقعرة في مجالها ولا توجد نقاط انقلاب.

نقطة الانقلاب: هي نقطة تنتمي لمنحني الدالة وتكون فيها المشتقة الثانية تساوي صفراً أو غير معرفة والتي تتغير فيها إشارة المشتقة الثانية من تحدب إلى تقعر أو بالعكس.

(1)- جد نقاط الانقلاب للمنحني: $f\left(x\right)=2x^3-3x^2-12x+1$

$\begin{array}{rl}& f^{\mathrm{\prime }}\left(x\right)=6x^2-6x-12\\ & f^{\prime \prime }\left(x\right)=12x-6 \left(f^{\prime \prime }\left(x\right)=0 \left(\mathrm{نجعل}\right)\right)\\ & 12x-6=0\Rightarrow 12x=6\Rightarrow x=\frac{1}{2}\\ & f\left(\frac{1}{2}\right)=2{\left(\frac{1}{2}\right)}^3-3{\left(\frac{1}{2}\right)}^2-12\left(\frac{1}{2}\right)+1=\frac{-11}{2}\end{array}$

$f$ مقعرة في $\{x:x>\frac{1}{2}\}$ لأن $f^{\prime \prime }\left(x\right)$ موجبة.

$f$ محددبة في $\{x:x<\frac{1}{2}\}$ لأن $f^{\prime \prime }\left(x\right)$ سالبة.

النقطة $(\frac{1}{2},\frac{-11}{2})$ هي نقطة انقلاب.

(2)- جد مناطق التقعر والتحدب ونقاط الانقلاب (إن وجدت) للدوال الآتية:

$f\left(x\right)=4x^3-x^4$

$\begin{array}{rl}& f\text{'}\left(x\right)=12x^2-4x^3\\ & f^{\prime \prime }\left(x\right)=24x-12x^2\left(f^{\prime \prime }\right(x)=0 \left(\mathrm{نجعل}\right))\\ & [24x-12x^2=0]÷12\Rightarrow 2x-x^2=0\\ & x(2-x)=0\\ & either x=0\\ & \text{or }2-x=0\Rightarrow x=2\end{array}$

نقطة انقلاب $\left(0,0\right)$

$f\left(0\right)=4(0{)}^3-(0{)}^4=0$

نقطة انقلاب $\left(2,16\right)$

$f\left(2\right)=4(2{)}^3-(2{)}^4=32-16=16$

مقعرة في الفترة $(0,2)$

محدبة في $\{x:x<0\} , \{x:x>2\}$

$f\left(x\right)=x+\frac{1}{x} , x\ne 0$

$\begin{array}{rl}& f\left(x\right)=x+x^{-1}\Rightarrow f\text{'}\left(x\right)=1-x^{-2}\\ & f\text{'}\text{'}\left(x\right)=2x^{-3}\\ & f^{\prime \prime }\left(x\right)=\frac{2}{x^3}\ne 0\left(f^{\prime \prime }\right(x)=0 \left(\mathrm{نجعل}\right))\end{array}$

لا توجد نقاط انقلاب لأن 0 لا ينتمي لمجال الدالة فنجعل المقام = 0

$x^3=0\Rightarrow x=0$

$f$ مقعرة في $\{x:x>0\}$

$f$ محددبة في $\{x:x<0\}$

ملاحظة: الحالات الثلاث التي تنطبق على $f\text{'}\left(x\right)$ والتي تجعلها لا تساوي صفراً هي نفسها تنطبق على $f^{\prime \prime }\left(x\right)$ وكذلك ملاحظة تنطبق على $f\left(x\right)$.

ملاحظة: يستفاد من نقطة الانقلاب في إيجاد الثوابت كما هو الحال في النقطة الحرجة.

$h\left(x\right)=4-(x+2{)}^4$

$\begin{array}{rl}& h\text{'}\left(x\right)=-4(x+2{)}^3\\ & h\text{'}\text{'}\left(x\right)=-12(x+2{)}^2\left(h^{\prime \prime }\right(x)=0 \left(\mathrm{نجعل}\right))\\ & [-12(x+2{)}^2=0]÷(-12)\Rightarrow (x+2{)}^2=0 \left(\mathrm{التربيعي} \mathrm{بالجذر}\right)\\ & \therefore x+2=0\Rightarrow x=-2\end{array}$

لا توجد نقاط انقلاب عند $x=-2$

$h$ محدبة في $\{x:x>-2\} , \{x:x<-2\}$

$f\left(x\right)=3-2x-x^2$

$\begin{array}{rl}& f\text{'}\left(x\right)=-2-2x\\ & f\text{'}\text{'}\left(x\right)=-2<0\therefore f\text{'}\text{'}\left(x\right)\ne 0\end{array}$

لا توجد نقاط انقلاب والدالة $f$ محدبة $\mathrm{\forall }x\in R$

$f\left(x\right)=x^4+3x^2+3$

$\begin{array}{rl}& f\text{'}\left(x\right)=4x^3+6x\\ & f\text{'}\text{'}\left(x\right)=12x^2+6>0(f\text{'}\text{'}(x)\ne 0)\end{array}$

لا توجد نقاط انقلاب والدالة $f$ مقعرة $\mathrm{\forall }x\in R$