مثل العمليات الآتية هندسياً في شكل (أرجاند).

$(6-2i)-(2-5i)$

$\begin{array}{rl}& z_1+(-z_2)=(6-2i)+(-2+5i)\\ & z_1=6-2i\Rightarrow P_1(6,-2)\\ & z_2=2-5i\Rightarrow P_2(-2,5)\\ & z_1+z_2=z_3=(4+3i)\Rightarrow P_3(4,3)\end{array}$

ملاحظة:

• العدد Z نظيره Z- يعني إذا كانت $Z=1+2i$ فإن $-Z=-1-2i$
• للعدد Z المرافق هو $\overline{Z}$ ويقصد به تغيير إشارة الوسط فقط $Z=1+2i , \overline{Z}=1-2i$

التمثيل الهندسي للأعداد المركبة

التمثيل الهندسي للأعداد المركبة

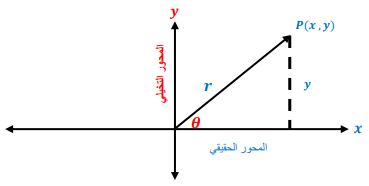
العدد المركب $(x+yi)$ يمكن تمثيله هندسياً بالنقطة $(x,y)$ حيث يسمى المحور $(x-\text{axis})$ بالمحور الحقيقي وهو يمثل الجزء الحقيقي للعدد المركب، أما المحور $(y-\text{axis})$ فيسمى المحور التخيلي وهو يمثل الجزء التخيلي للعدد المركب، ويمكن تمثيل بعض العمليات التي تجري على الأعداد المركبة تمثيلاً هندسياً وتسمى الأشكال الناتجة بأشكال (أرجاند) ويسمى المستوي الذي يحتويها بالمستوى المركب وسترمز لها بالرمز $P(x,y)$.

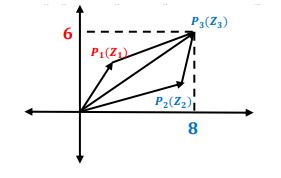
إذا كان $z_2=x_2+y_{2}i , z_1=x_1+y_{1}i$ عددان مركبان ممثلان بالنقطتين $P_1(x_1,y_1)\hspace{0.17em}, P_2(x_2,y_2)$ فإن:

$z_1+z_2=(x_1+x_2)+(y_1+y_2)i$

ويمكن تمثيل $z_1+z_2$ بالنقطة $P_3=(x_1+x_2,y_1+y_2)$ وذلك باستخدام المعلومات المتعلقة بالمتجهات وكما موضح بالشكل:

أي أن: $\overrightarrow{O{P}_1}+\overrightarrow{O{P}_2}=\overrightarrow{O{P}_3}$

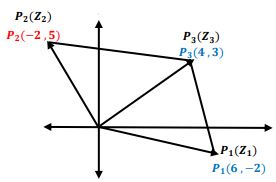
(1)- مثل العمليات الآتية هندسياً في شكل (أرجاند).

$(3+4i)+(5+2i)$

$\begin{array}{rl}& z_1=3+4i\Rightarrow P_1(3,4)\\ & z_2=5+2i\Rightarrow P_2(5,2)\\ & z_1+z_2=(3+4i)+(5+2i)\\ & z_1+z_2=z_3=(8+6i)\Rightarrow P_3(8,6)\end{array}$

$(6-2i)-(2-5i)$

$\begin{array}{rl}& z_1+(-z_2)=(6-2i)+(-2+5i)\\ & z_1=6-2i\Rightarrow P_1(6,-2)\\ & z_2=2-5i\Rightarrow P_2(-2,5)\\ & z_1+z_2=z_3=(4+3i)\Rightarrow P_3(4,3)\end{array}$

ملاحظة:

• العدد Z نظيره Z- يعني إذا كانت $Z=1+2i$ فإن $-Z=-1-2i$
• للعدد Z المرافق هو $\overline{Z}$ ويقصد به تغيير إشارة الوسط فقط $Z=1+2i , \overline{Z}=1-2i$