جد القيمة العددية للمقدار:

${(\tan {60}^{\circ })}^2+{(\cot {45}^{\circ })}^2+{(\sec {30}^{\circ })}^2+{(\sin {45}^{\circ })}^2$

$\begin{array}{rl}& \tan 60=\sqrt{3} , \cot 45=1 , \sec 30=\frac{2}{\sqrt{3}} , \sin 45=\frac{1}{\sqrt{3}}\\ & (\sqrt{3}{)}^2+(1{)}^2+{\left(\frac{2}{\sqrt{3}}\right)}^2+{\left(\frac{1}{\sqrt{3}}\right)}^2\Rightarrow 3+1+\frac{4}{3}+\frac{1}{2}\\ & 4+\frac{8+3}{6}\Rightarrow 4+\frac{11}{6}\Rightarrow \frac{24+11}{6}=\frac{35}{6}\end{array}$

مراجعة الفصل

(1)- مثل المعادلة 1+y=2x في المستوي الإحداثي.

(2)- مثل المعادلة 1+y=3x² في المستوي الإحداثي.

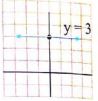
(3)- مثل المعادلة y=3 في المستوي الإحداثي.

(4)- مثل المعادلة x=3 في المستوي الإحداثي.

(1)- جد ميل المستقيم المار بالنقطتين:

i) (- 2,1), (6,7)

$\mathrm{m}=\frac{7-1}{6+2}=\frac{6}{8}=\frac{3}{4}$

ii) (4,2), (1,2)

$\mathrm{m}=\frac{2-2}{1-4}=0$

iii) (4,2), (4,-1)

$m=\frac{-1-2}{4-4}$

غير معرف.

(2)- جد المقطع السيني والصادي لكل معادلة مما يأتي:

i) 2x-y=-4

• المقطع السيني: 2.
• المقطع الصادي: 4-.

ii) y=-5

• المقطع السيني: لا يوجد.
• المقطع الصادي: 5-.

iii) x=-5

• المقطع السيني: 5-.
• المقطع الصادي: لا يوجد.

(1)- جد معادلة المستقيم المار بالنقطتين:

(2-,1) ,(3,4)

$\begin{array}{rl}& \frac{\mathrm{y}-{\mathrm{y}}_1}{\mathrm{x}-{\mathrm{x}}_1}=\frac{{\mathrm{y}}_2-{\mathrm{y}}_1}{{\mathrm{x}}_2-{\mathrm{x}}_1}\Rightarrow \frac{\mathrm{y}-4}{\mathrm{x}-3}=\frac{1-4}{-2-3}=\frac{-3}{-5}\\ & 5\mathrm{y}-20=3\mathrm{x}-9\Rightarrow 5\mathrm{y}-3\mathrm{x}=11\end{array}$

(2)- جد معادلة المستقيم الذي ميله ($\frac{-1}{3}$) ومقطعه السيني يساوي (7)

$\mathrm{y}-{\mathrm{y}}_1=\mathrm{m}(\mathrm{x}-{\mathrm{x}}_1)⟹\mathrm{y}-7=-\frac{1}{3}(\mathrm{x}-0)⟹3\mathrm{y}+\mathrm{x}=21$

(3)- جد الميل والمقطع الصادي للمستقيم الذي معادلته 2x-4y=8

$\begin{array}{rl}& 2\mathrm{x}-4\mathrm{y}=8⟹4\mathrm{y}=2\mathrm{x}-8\Rightarrow \mathrm{y}=\frac{1}{2}\mathrm{x}-2\\ & \mathrm{m}=\frac{1}{2}\end{array}$

والمقطع الصادي 2-

(1)- برهن أن الشكل ABCD الذي رؤوسه:

(3 -,1) A (3,1), B (-1,3), C (-3,1), D متوازي أضلاع.

$$\begin{gathered} \begin{array}{rl}& {\mathrm{m}}_{\mathrm{AB}}\frac{3-1}{-1-3}=\frac{2}{-4}=-\frac{1}{2}\\ & {\mathrm{m}}_{1\mathrm{C}}\frac{-1+3}{-3-1}=\frac{2}{-4}=-\frac{1}{2}\end{array} \\ {\mathrm{m}}_{\mathrm{AD}}=\frac{-3-1}{1-3}=\frac{-4}{-2}=2,{\mathrm{m}}_{\mathrm{BC}}=\frac{-1-3}{-3+1}=\frac{-4}{-2}=2 \\ \overline{\mathrm{AD}}//\overline{\mathrm{BC}} \end{gathered}$$

الشكل متوازي الأضلاع.

(2)- بين أن النقط: (6,4) ,(4,0) ,(6-,1) تقع على استقامة واحدة.

$\begin{array}{rl}& \mathrm{A}(1,-6),\mathrm{B}(4,0),\mathrm{C}(6,4)\\ & {\mathrm{m}}_{\mathrm{AB}}=\frac{0+6}{4-1}=\frac{6}{3}=2 , {\mathrm{m}}_{\mathrm{BC}}=\frac{4-0}{6-4}=\frac{4}{2}=2\end{array}$

النقاط تقع على استقامة واحدة.

(3)- بين أن المثلث الذي رؤوسه:

A (0,-4), B (-1,0), C (7,2) مثلث قائم الزاوية.

$\begin{array}{rl}& {\mathrm{m}}_{\mathrm{AB}}=\frac{0+4}{-1-0}=\frac{4}{-1}=-4\\ & {\mathrm{m}}_{\mathrm{BC}}=\frac{2-0}{7+1}=\frac{2}{8}=\frac{1}{4}\\ & \overline{\mathrm{AB}}\perp \overline{\mathrm{BC}}\end{array}$

(1)- جد نقطة منتصف للقطعة المستقيمة AB

A (-2,0), B (4,5)

$\mathrm{M}=(\frac{{\mathrm{x}}_1-{\mathrm{x}}_2}{2},\frac{{\mathrm{y}}_1-{\mathrm{y}}_2}{2})\Rightarrow \mathrm{M}=(\frac{-2+4}{2},\frac{0+5}{2})=(1,\frac{5}{2})$

(2)- هل النقط (2-,2-) A (0,1), B (3,-1), C تمثل رؤوس مثلث قائم الزاوية؟

$\begin{array}{rl}& \mathrm{AB}=\sqrt{{({\mathrm{x}}_2-{\mathrm{x}}_1)}^2{({\mathrm{y}}_2-{\mathrm{y}}_1)}^2}=\sqrt{(3-0{)}^2(-1-1{)}^2}=\sqrt{9+4}=\sqrt{13}\\ & \mathrm{BC}=\sqrt{(-2-3{)}^2(-2+1{)}^2}=\sqrt{25+1}=\sqrt{26}\\ & \mathrm{AC}=\sqrt{(-2-0{)}^2(-2-1{)}^2}=\sqrt{4+9}=\sqrt{13}\\ & \left(\mathrm{BC}{)}^2\stackrel{?}{=}\right(\mathrm{AB}{)}^2+(\mathrm{AC}{)}^2\Rightarrow (\sqrt{26}{)}^2=(\sqrt{13}{)}^2+(\sqrt{13}{)}^2\end{array}$

المثلث قائم الزاوية حسب عكس فيثاغورس.

(3)- باستعمال قانون المسافة بين هل النقط A (-1,-3), B (-6,1), C (-3,3) تقع على استقامة واحدة؟

$\begin{array}{rl}& \mathrm{AB}=\sqrt{(1+3{)}^2(-6+1{)}^2}=\sqrt{16+25}=\sqrt{41}\\ & \mathrm{BC}=\sqrt{(3-1{)}^2(-3+6{)}^2}=\sqrt{4+9}=\sqrt{13}\\ & \mathrm{AC}=\sqrt{(3+3{)}^2(-3+1{)}^2}=\sqrt{36+4}=\sqrt{40}\\ & \sqrt{41}\ne \sqrt{40}+\sqrt{13}\end{array}$

النقاط تقع على استقامة واحدة.

(1)- المثلث ABC القائم الزاوية في B إذا كانت:

tan C=1 جد:

$\begin{array}{rl}& \tan c=\frac{1}{1}\\ & (\mathrm{AC}{)}^2=(1{)}^2+(1{)}^2 \Rightarrow \mathrm{AC}=\sqrt{2}\end{array}$

i) cotC

$\cot C=1$

ii) sinC

$\sin \mathrm{C}=\frac{1}{\sqrt{2}}$

iii) secA

$\sec \mathrm{A}=\sqrt{2}$

iv) cscC

$\csc \mathrm{C}=\sqrt{2}$

v) cosA

$\cos \mathrm{A}=\frac{1}{\sqrt{2}}$

(2)- جد القيمة العددية للمقدار:

${(\tan {60}^{\circ })}^2+{(\cot {45}^{\circ })}^2+{(\sec {30}^{\circ })}^2+{(\sin {45}^{\circ })}^2$

$\begin{array}{rl}& \tan 60=\sqrt{3} , \cot 45=1 , \sec 30=\frac{2}{\sqrt{3}} , \sin 45=\frac{1}{\sqrt{3}}\\ & (\sqrt{3}{)}^2+(1{)}^2+{\left(\frac{2}{\sqrt{3}}\right)}^2+{\left(\frac{1}{\sqrt{3}}\right)}^2\Rightarrow 3+1+\frac{4}{3}+\frac{1}{2}\\ & 4+\frac{8+3}{6}\Rightarrow 4+\frac{11}{6}\Rightarrow \frac{24+11}{6}=\frac{35}{6}\end{array}$

(3)- أثبت أن:

i) ${(\csc {30}^{\circ })}^2+{(\cot {30}^{\circ })}^2=7$

$\text{L. S}=(2{)}^2+(\sqrt{3}{)}^2\Rightarrow 4+3=7=\text{R.S}$

ii)$2\sin {45}^{\circ }\cos {45}^{\circ }=\sin {90}^{\circ }$

$$\begin{gathered} \mathrm{L}.\mathrm{S}=2\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right)=2\frac{1}{2}=1 \\ \text{R.}\mathrm{S}=\sin {90}^{\circ }=1 \\ \mathrm{L}.\mathrm{S}=\mathrm{R}\cdot \mathrm{S} \end{gathered}$$

iii) ${(\cos {60}^{\circ })}^2-{(\sin {60}^{\circ })}^2=-\frac{1}{2}$

$\text{ L.S}={\left(\frac{1}{2}\right)}^2-{\left(\frac{\sqrt{3}}{2}\right)}^2\Rightarrow \frac{1}{4}-\frac{3}{4}=\frac{-2}{4}=-\frac{1}{2}=\mathrm{R}.\mathrm{S}$