تمرينات (2 - 7)
(1)-
أ) أوجد المدى للقيم التالية: 12، 9، 7، 8، 0، 3
المدى R
ب) أوجد المدى من الجدول التالي:
المدى = الحد الأعلى للفئة الأخيرة - الحد الأدنى للفئة الأولى + 1
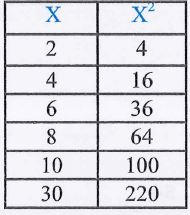
(2)- عرف الإنحراف المعياري ثم احسب الإنحراف المعياري للقيم التالية: 2، 4، 6، 8، 10
الإنحراف المعياري: هو القيمة الموجبة للجذر التربيعي لمتوسط مربعات إنحرافات قيم مفردات التوزيع عن وسطها الحسابي ويرمز له بالرمز (S).
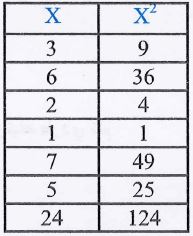
(3)- أوجد الإنحراف المعياري للأعداد: 3، 6، 2، 1، 7، 5 ثم أضف 5 إلى كل عدد منها وأثبت أن هذه الإضافة لا تؤثر على قيمة الإنحراف المعياري ولكنها تؤثر على قيمة الوسط الحسابي.
لاحظ أن الوسط الحسابي x قد تغير
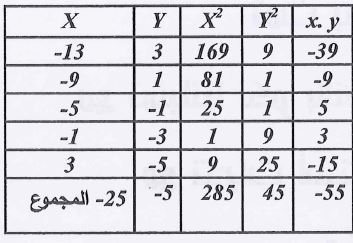
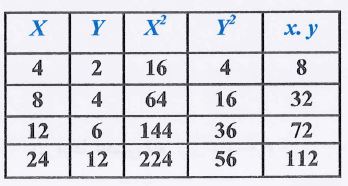
(4)- جد معامل الارتباط بين المتغيرين x ،y ثم بين نوعه؟
الارتباط طردي تام
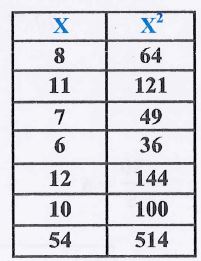
(5)- في السؤال السابق لو ضربت قيم x في 4 تحصل على جدول آخر، جد معامل الارتباط للقيم الجديدة وقارن النتيجة بالسؤال السابق.
نلاحظ أن لو ضربت قيم أحد المتغيرين في عدد ما لم يتغير معامل الارتباط.

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)