تمرينات (4 - 6)
(1)- 1- جد معادلة المستقيم الذي ميله ويمر بالنقطة (0 ,4 -).
ملاحظة: دائماً حاول أن ترتيب معادلة المستقيم بالشكل
2- جد معادلة المستقيم الموازي لمحور السينات ويمر بالنقطة (1- ,2).
المستقيم الذي محور السينات ميله = 0 لذلك
3- جد معادلة المستقيم الموازي لمحور الصادات ويمر بالنقطة (1- ,2).
إذا كان المستقيم // محور الصادات فإن y-y1=0 لذلك.
يحذف الميل لأنه غير معرف (لا يوجد ميل).
4- جد معادلة المستقيم المار بالنقطتين (3 ,1-)، (5 ,1-).
5- جد معادلة المستقيم L المار بالنقطة (1- ,2) والموازي إلى الذي ميله .
- إذا توازى مستقيمان فأن ميلاهما متساوي
- ميل L = ميل L1 لأن لذلك
6- جد معادلة المستقيم المار بالنقطة (2- ,0) وعمودياً على المستقيم الذي ميله .
إذا تعامد مستقيمان فإن حاصل ضرب ميلهما = 1- أي:
ملاحظة: عزيزي الطالب يمكن إيجاده مباشرة إذا تعامد مستقيمان وأعطاك ميل أحدهما فإن ميل الثاني يساوي (- مقلوب ميل المستقيم الأول).
7- جد معادلة المستقيم المار بالنقطة (4- ,3) وعمودياً على المستقيم المار بالنقطتين (2- ,2)، (3, 0).
ميل المستقيم المار بالنقطتين:
ميل المستقيم المطلوب والمار بالنقطة (4- ،3) هو
8- لتكن جد معادلة المستقيم العمود الذي ينصف
لتكن C منتصف
(2)- 1- جد معادلة المستقيم الذي ميله = 3- ويقطع جزءاً موجباً من محور الصادات طوله 7 وحدات
نقطة التقاطع مع محور الصادات نفرض x = 0 فتكون (7 ،0) والميل = 3- فتكون معادلة المستقيم:
2- جد معادلة المستقيم الذي ميله = 2 ويقطع جزءاً سالباً من محور السينات طوله 6 وحدات.
نقطة التقاطع مع محور السينات نفرض y = 0 فتكون (0 ،6-) والميل = 2 فتكون معادلة المستقيم:
3- جد الميل والجزء المقطوع من محور الصادات لكل مستقيم فيما يأتي:
أ)
أما الجزء المقطوع من محور الصادات بفرض x = 0
ب)
ج)
4- جد معادلة المستقيم المار بالنقطة (5- ,2) ويوازي المستقيم الذي معادلته: 2x - y + 3 = 0
نجد ميل المستقيم المعلوم فإن 2x - y + 3 = 0 فإن:
معادلة المستقيم الذي يمر بالنقطة (5- ،2) هي:
5- جد معادلة المستقيم L الذي يقطع جزءاً سالباً من محور الصادات طوله 4 وحدات وعمودياً على المستقيم 2y = 4 x -1.
نجد نقطة التقاطع للمستقيم L الذي يقطع محور الصادات بفرض x = 0
نقطة التقاطع (4- ،0) ونجد الميل للمستقيم المعلوم حيث تصبح المعادلة:
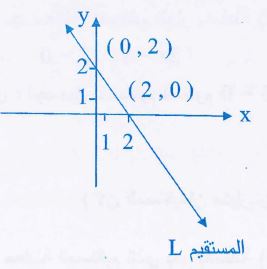
6- ليكن مستقيماً معادلته: 0 = x + y -2 جد ميله ونقطة تقاطعه مع محور الصادات ثم ارسم .
ونقطة تقاطعه مع محور الصادات بفرض x = 0 فإن:
نقطة التقاطع (2 ،0) مع محور الصادات.
ونفرض
فنقطة التقاطع مع محور السينات (0 ،2) والرسم:
7- جد معادلة المستقيم L المغنار بالنقطة (2- , 2) وعمودياً على المستقيم الذي معادلته x + y = 0 ثم جد نقطة تقاطع المستقيم L مع المحورين الإحداثيين.
نجد ميل المستقيم المعلوم x = y = 0 فإن:
نجد نقطتي التقاطع لهذا المستقيم مع المحورين: بفرض x = 0 فإن: نقطة التقاطع مع محور السينات (0 ،4)
8- المستقيم : 2x - y = 3 والمستقيم
أ) بين أن
ب) جد جبرياً نقطة تقاطع المستقيمين. L، H
9- جد معادلة المستقيم الذي يصنع 135 ˚ مع الاتجاه الموجب لمحور السينات والمار بنقطة الأصل.
الميل = ظل زاوية المستقيم التي يضعها المستقيم مع الاتجاه الموجب لمحور السينات:
نجد معادلة المستقيم الذي ميله (1-) ومار بنقطة الأصل (0 ،0):
10- المستقيم يمر بالنقطة (2 ,1) جد:
أ) a ∈ R
بما أن المستقيم يمر بالنقطة (2 ،1) فأنها تحقق المعادلة

.JPG)