تمرينات (2 - 6)
.JPG)
(1)- جد إحداثيات النقطة التي تقسم القطعة المستقيمة A B، حيث A (1 ،3) ،B (4 ،6) بنسبة .
(2)- جد إحداثيات النقطة التي تنصف قطعة المستقيم AB حيث أن A (2 ,-4) ،B (-3 ,-6).
(3)- جد إحداثيات النقطة C التي تقسم قطعة المستقيم AB بنسبة حيث أن A (2 ,1) ،B (1,-3).
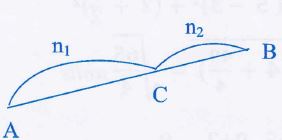
(4)- جد إحداثيات النقطة C التي تبعد عن A ثلاثة أمثال بعدها عن B حيث A (2 , 6) ،B (4 ,-4).
(5)- جد إحداثيات منتصفات أضلاع A B CΔ حيث A (4 ,0) ،B (5 ,2) ،C (2 ,-3) ثم جد أطوال المستقيمات الواصلة بين رؤوس المثلث ومنتصفات الأضلاع المقابلة.
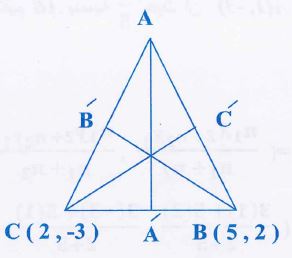
Aَ منتصف ، َB منتصف ، َC منتصف
(6)- بين أن قطري الشكل الرباعي الذي رؤوسه (8-, 5-)، (3-, 3-)، (3, 1)، (2-, 1-) ينصف أحدهما الآخر.
.JPG)
نفرض أن نقطة منتصفي القطرين (0)
مشاركة الدرس

.JPG)


.JPG)