رسم على ورق المربعات الأشكال المبينة أدناه، ثم ارسم صور تمددها باستعمال المعلومات الواردة أسفل كل شكل

مركز التمدد B معامل التمدد $\frac{1}{4}$

تدرب وحل التمرينات

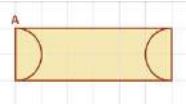
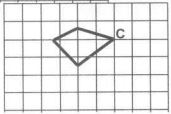
(3)- ارسم على ورق المربعات الأشكال المبينة أدناه، ثم ارسم صور تمددها باستعمال المعلومات الواردة أسفل كل شكل.

مركز التمدد A معامل التمدد 2

مركز التمدد B معامل التمدد $\frac{1}{4}$

مركز التمدد C معامل التمدد $\frac{2}{5}$

(4)- جد الإحداثيات الناتجة عن تمدد الشكل الرباعي ABCD في كل من الحالات التالية باستعمال معامل التمدد المؤشرة إزاء كل حالة، إذا كان مركز التمدد هو نقطة الأصل.

A (0,3), B (2,1), C (0,-2) D (-2,-1) (i ومعامل التمدد =4.

$\begin{array}{r}A(0,3)\Rightarrow A^{\mathrm{\prime }}(0,12)\\ B(2,1)\Rightarrow B^{\mathrm{\prime }}(8,4)\end{array}$

يضرب المعامل في كل من الإحداثي السيني والصادي لنحصل على صورة النقطة الجديدة.

$\begin{array}{rl}& C(0,-2)\Rightarrow C^{\mathrm{\prime }}(0,-8)\\ & D(-2,-1)\Rightarrow D^{\mathrm{\prime }}(-8,-4)\end{array}$

A (-3,2), B (3,3), C (5,-2), D (-2,0) (ii ومعامل التمدد =$\frac{2}{3}$.

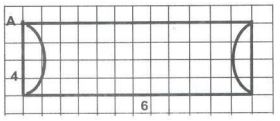
(5)- إذا علمت أن أحد المضلعين في الشكل المجاور هو تمدد للمضلع الآخر، استخرج معامل التمدد وبين فيما إذا كان تكبيراً أم تصغيراً.

احسب الأطوال من الشكل

$\frac{PR}{P^{\mathrm{\prime }}{R}^{\mathrm{\prime }}}=\frac{2}{4}=\frac{1}{2}=\frac{aS}{a^{\mathrm{\prime }}{S}^{\mathrm{\prime }}}$

نلاحظ أن معامل التمدد في كتابة النسب بين الأضلاع المتناظرة عدد ثابت = $\frac{1}{2}$

$\frac{PQ}{P^{\mathrm{\prime }}{Q}^{\mathrm{\prime }}}=\frac{1.5}{3}=\frac{1}{2}=\frac{RS}{R^{\mathrm{\prime }}{S}^{\mathrm{\prime }}}$

معامل التمدد هو $\frac{1}{2}$ وهو تصغير لأن المعامل أصغر من 1 وأكبر من 0.